Solver Max - Warehouse space for free: Non-linear model

11 March 2024

A common problem for warehouse managers is finding enough space to store everything:

We just don't have enough storage space. There used to be, but the company grew. Now, we have pallets stored in the dispatch area. They get in the way, and it's a health and safety hazard.
Warehouse Manager

In this article series, we look at improving the efficiency of a pallet warehouse (also known as a unit-load warehouse), where all items are stored on standard-size pallets.

Most pallet warehouses use a rack design where all shelves are the same size. This may not be the best design. Specifically, if the pallets have varying heights, then a single shelf height – designed to accommodate the tallest pallet – leaves unused space above some pallets. Depending on the mix of pallet heights, there's potentially a lot of unused space in aggregate.

To address this issue, we build a model of the warehouse's racks and shelves. Our objective is to find a design that minimizes the number of racks required to accommodate all pallets in the warehouse.

Along the way, we:

Formulate a non-linear model of the situation.
Compare several solvers, to see how they perform.
Linearize our model to, hopefully, make it easier to solve.
Disaggregate our model to make some variables exogenous, then iterate over an enumeration of the exogenous variables.
Demonstrate use of Pyomo's last() and next() functions, which enable us to work with elements of ordered sets.
Turn off a constraint using Pyomo's deactivate() function.

Importantly, we show that there's a surprising amount of extra storage space available for free, or minimal cost, just by redesigning the warehouse's racks and shelves.

Download the models

The models described in this series of articles are built in Python using the Pyomo library.

The files are available on GitHub.

Situation

We're working with the managers of a pallet warehouse that has the capacity to store 20,000 pallets on 1,000 racks. Each rack is currently configured with 5 shelves. Each shelf has a fixed width that has slots for 4 pallets. The shelves are one pallet deep.

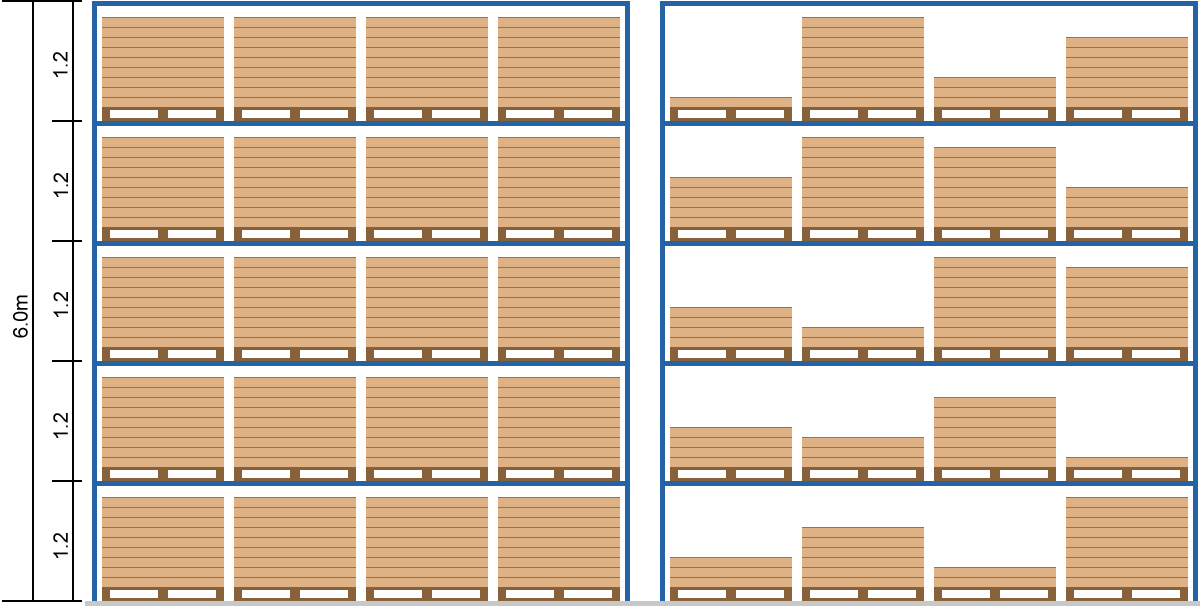
Figure 1 shows two example racks. Each rack has a fixed height of 6.0m. Each of the 5 shelves is 1.2m high, able to accommodate a 1.0m high pallet (the wooden pallet itself, plus the product), and a gap with sufficient room for the pallet forklift to manoeuvre pallets into and out of the slots.

It seems that our warehouse was designed with the assumption that every pallet is the full 1.0m high, like the rack on the left of Figure 1. These pallets utilize 100% of the space available in this rack.

But, in practice, that assumption isn't correct – not even close. Pallets have a variety of heights, like the rack on the right of Figure 1, either because products vary in their height or because some pallets hold products that have been partially used. Although all of the slots are occupied, these pallets utilize only 63% of the space available in the rack on the right.

Figure 1. Current rack design (left) and actual usage (right)

Academic literature

There is a large academic literature looking at various aspects of warehouse efficiency.

A search of the academic literature identies a similar situation discussed in the paper How to determine slot sizes in a unit-load warehouse. That paper uses a complex, stochastic optimization methodology, as summarized in the blog post Finding warehouse space in unexpected places.

We use a simpler, deterministic approach – initially using a Mixed Integer Non-Linear Program, which we'll later linearize.

Model 1 design

Compress the pallets into fewer racks

The Warehouse Manager's most pressing issue is that the warehouse is operating beyond its design capacity. We need to find additional space, but renting a larger warehouse would be expensive. Before we consider other warehouse options, we want to explore redesigning the current warehouse to see if we can use the existing space more efficiently.

Our racks are configurable, meaning that the vertical position of the shelves can be changed in 0.1m increments. The total height must be 6.0m, as the racks have bracing across the top for strength and stability. To avoid over-complicating the warehouse operation, the Warehouse Manager wants all racks to have the same design.

The basic idea for our modelling is that instead of having 5 x 1.2m shelves, we can have 6 or more shelves including some smaller shelves. Having more shelves would increase the number of pallet slots per rack. That is, we want to take advantage of the pallet height variation, compressing the pallets into fewer racks.

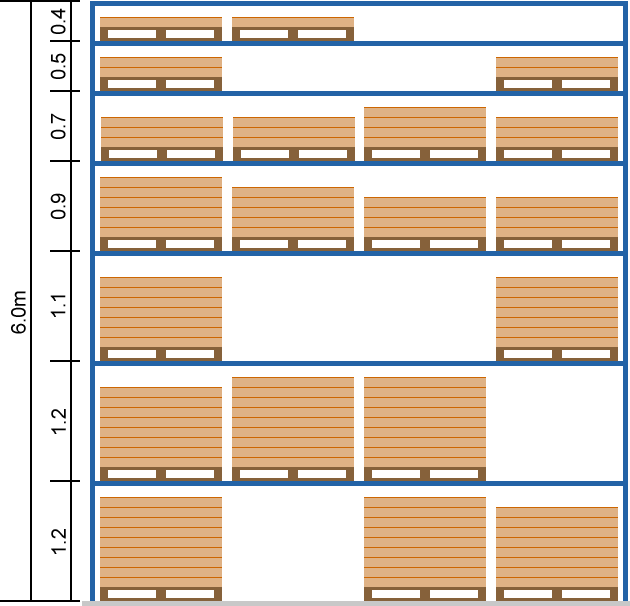
Specifically, we want to minimize the number of racks needed to store all the pallets. For example, Figure 2 shows an alternative rack design. This rack has 7 shelves, with 28 slots, compared with our current design, which has 5 shelves with 20 slots per rack.

The pallets from the right-hand-side of Figure 1 have been positioned on this alternative design. There are 8 empty slots that we could fill with pallets from other racks. If we do that many times, then we will need significantly fewer racks to store all the pallets. Alternatively, we could retain the same number of racks, but have more slots available to store more pallets. Or we could adopt some solution in between.

Of course, if we increase the number of shelves per rack and increase the number of racks, then we would need to purchase additional shelves. But additional shelving is considerably cheaper than moving to, and then operating, a larger warehouse.

Design criteria

In designing the racks, we need to consider the following criteria:

The racks have a fixed height of 6.0m.
Shelves can be positioned vertically in 0.1m intervals.
The floor at the base of a rack is counted as a shelf.
A wooden pallet is 140mm high. To simplify the modelling, we'll assume that a pallet is 0.1m high, then include the extra 40mm in the "gap" above the pallet.
The products on a pallet can vary from 0.1m high to 0.9m high, in increments of 0.1m. Therefore, including the pallet itself, shelves need to accommodate heights from 0.2m to 1.0m.
Pallets cannot be stacked on top of other pallets.
The shelves, and the bracing across the top of each rack, are made from 60mm hollow square steel tubing.
The warehouse uses specialist pallet forklifts for loading and unloading pallets. The forklift requires 100mm clearance between the top of a pallet's products and the shelf (or rack top) above.
In total, each shelf needs an extra 0.2m, to allow for: 0.1m loading/unloading clearance, 0.06m shelf height, and the 0.04m not counted in the wooden pallet's height (as mentioned above). We refer to this 0.2m as the "gap" between shelves.

Crucially, the warehouse needs to accommodate our mix of pallets. A census of the current 20,000 pallets produces the distribution shown in Figure 3.

This distribution has two peaks, due to:

Many products using the full 1.0m available height. Some of these are a fixed 1.0m high, while others are consumable.
Some products are initially only 0.5m high.
Some pallets have products that have been opened and partially consumed, reducing their height.
The minimum height of a pallet is 0.2m, being the pallet itself and 1 x 0.1m layer of product.

Figure 3. Distribution of pallet heights

Decisions to be made

At first glance, this situation seems straightforward. In designing the racks, our model just needs to make the following decisions:

The number of shelves in a rack.
The height of each shelf.
The number of racks.

But embedded in this situation is the need to pack the 20,000 pallets into the shelves. In general, packing problems can be difficult to solve. Here the "bins" we're packing into are a moving target, as the rack and shelf specifications are also variables being decided by the model. With so many moving parts, this situation might be more difficult than it seems.

In any case, our objective is simple: minimize the number of racks required to store the existing 20,000 pallets.

As the warehouse is currently over capacity, we also have some pallets stored in the warehouse's dispatch area (much to the annoyance of the Packing & Dispatch Manager). We assume that the extra pallets have the same height distribution. Even if that assumption isn't correct, there are relatively few of these pallets, so the difference is not material.

Model 1 Formulation

We formulate Model 1 as shown in Figure 4. That is:

Equation (1). The objective function is to minimize the number of racks needed to store the pallets. We have an option to use a weighted average of the number of racks and the number of shelves. By using carefully chosen weights, that objective will have a value like 1000.5, representing 1,000 racks of 5 shelves each.
Equation (2). Each pallet must be allocated to a shelf that is at least the height of the pallet.
Equation (3). Each pallet must be allocated to exactly one shelf.
Equation (4). For each shelf, the allocation must be within the number of available slots.
Equation (5). Total height of shelves in a rack, plus gaps between shelves, must equal the rack height.
Equation (6). Each shelf can be no higher than the maximum.
Equation (7). Indicate that we're using an available shelf slot only if we allocate a pallet to that slot.
Equation (8). Order shelf sizes from largest to smallest.

Figure 4. Model 1 formulation

\begin{alignat}{1} &\text{Objective}\\ &\quad \text{Minimize} \quad Objective \quad &= &\quad \text{WeightRacks} \times Racks \\&&&\quad + \ \text{WeightShelves} \times \sum_{s=1}^{n} Shelf_{s} \tag{1} \\ \\ &\text{Subject to} \\ &\quad \text{Pallets}_{p} \quad &\le &\quad \sum_{s=1}^{n} ShelfHeights_{s} \times Allocation_{p, s} \quad &\forall \ p \in P \tag{2} \\ &\quad \sum_{s=1}^{n} Allocation_{p, s} \quad &= &\quad 1 \quad &\forall \ p \in P \tag{3} \\ &\quad \sum_{p=1}^{m} Allocation_{p, s} \quad &\le &\quad \text{PalletsPerShelf} \times Racks \quad &\forall \ s \in S \tag{4} \\ &\quad \text{RackHeight} &= &\quad \sum_{s=1}^{n} ShelfHeights_{s} + Shelf_{s} \times \text{Gap} \tag{5} \\ &\quad ShelfHeights_{s} \quad &\le &\quad Shelf_{s} \times \text{MaxShelfSize} \quad &\forall \ s \in S \tag{6} \\ &\quad \sum_{p=1}^{m} Allocation_{p, s} \quad &\ge &\quad Shelf_{s} \quad &\forall \ s \in S \tag{7} \\ &\quad ShelfHeights_{s} \quad &\ge &\quad ShelfHeights_{s+1} \quad &\forall \ s \in S_{n-1} \tag{8} \\ \\ &\text{Variables} \\ &\quad Racks \quad &= &\quad \text{Number of racks, positive integer} \tag{9} \\ &\quad Shelf_{s} \quad &= &\quad \text{Shelf is included in a rack, binary} \quad &\forall \ s \in S \tag{10} \\ &\quad ShelfHeights_{s} \quad &= &\quad \text{Height of each shelf, positive integer} \quad &\forall \ s \in S \tag{11} \\ &\quad Allocation_{p, s} \quad &= &\quad \text{Allocation of pallets to shelves, binary} \quad &\forall \ p \in P, \forall \ s \in S \tag{12} \\ \\ &\text{Data} \\ & \quad \text{WeightRacks} \quad &= &\quad \text{Objective weight for number of racks} \tag{13} \\ & \quad \text{WeightShelves} \quad &= &\quad \text{Objective weight for number of shelves} \tag{14} \\ & \quad \text{Pallets}_{p} \quad &= &\quad \text{Height of each pallet} \quad &\forall \ p \in P \tag{15} \\ & \quad \text{PalletsPerShelf} \quad &= &\quad \text{Number of pallets on each shelf} \tag{16} \\ & \quad \text{RackHeight} \quad &= &\quad \text{Height of each rack} \tag{17} \\ & \quad \text{Gap} \quad &= &\quad \text{Gap between shelves} \tag{18} \\ & \quad \text{MaxShelfSize} \quad &= &\quad \text{Maximum height of a shelf} \tag{19} \\ \\ &\text{Sets} \\ & \quad P && \quad \text{Pallet} \tag{20} \\ & \quad S && \quad \text{Shelf} \tag{21} \\ \\ &\text{Dimensions} \\ & \quad m && \quad \text{Number of pallets} \tag{22} \\ & \quad n && \quad \text{Number of shelves} \tag{23} \\ \end{alignat}

The model is non-linear because, in Equation (2), we multiply the decision variables for the shelf heights and the allocation of pallets to shelves. That is, the model needs to simultaneously decide the shelf heights and the specific pallets to assign to each shelf.

Note that Equation (8) sorts the shelf heights in descending order. We do this to reduce the number of possible solutions that are effectively the same. That is, we're indifferent between shelf sizes solutions of 5, 10, 7, 3, 10, 7, 4 and 10, 10, 7, 7, 5, 4, 3 and any other solution with the same shelf sizes in a different order. Eliminating the different, but equivalent, height orders hopefully makes it easier for the solver to find a solution. In practice, we'll put the larger shelf sizes at the bottom of a rack, to keep the rack's centre of gravity low – but that doesn't matter in the modelling. This type of "symmetry-breaking" constraint doesn't always help, so testing is required to see if it is useful for a particular model.

Model 1 implementation

Data

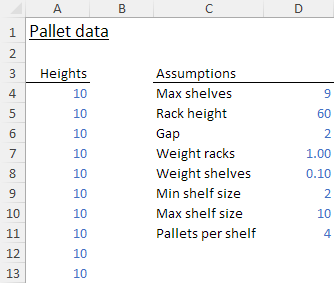
We need a list of heights for each pallet that must be packed into the shelves. This list is in an Excel file, with the first few rows shown in Figure 5. The heights are in descending order, though the order doesn't matter to the model.

We define our height variables as integers, to make them easier to work with. Therefore, all heights are defined in decimetres. For example, the racks are 6.0m high, which is expressed as 60 decimetres. Similarly, pallet heights vary from 2 to 10 decimetres (0.2m to 1.0m)

We also have several assumptions, each of which is in a named range. Specifically:

Max shelves. The maximum number of shelves in each rack. The current racks have 5 shelves. We allow for up to 9 shelves per rack, though the 2 decimetre gap required by each shelf makes it unlikely that 9 shelves is a viable solution.
Rack height. Total height of a rack. Defined in decimetres.
Gap. The gap between shelves. Defined in decimetres.
Weight racks. Objective function weight for the number of racks.
Weight shelves. Objective function weight for the number of shelves.
Min shelf size. Minimum height of a shelf's space for pallets. Defined in decimetres.
Max shelf size. Maximum height of a shelf's space for pallets. Defined in decimetres.
Pallets per shelf. Number of pallet slots on each shelf. This is fixed by the length of each rack.

Our full list of pallet sizes has 20,000 rows, being the capacity of the warehouse. Currently, the warehouse has 1,000 racks, each consisting of 5 shelves, with each shelf storing 4 pallets (i.e., 4 pallet slots per shelf * 5 shelves per rack * 1,000 racks = 20,000 pallets).

For testing purposes, we've created two samples of the pallet data: 200 pallets and 2,000 pallets. Given the current shelf design, 200 pallets require 10 racks and 2,000 pallets require 100 racks.

Symmetry-breaking constraint

Equation (8) orders the shelf sizes from largest to smallest. The idea is to reduce the number of size combinations. We implement this constraint as shown in Figure 6.

Figure 6. Symmetry-breaking constraint, Equation (8)

def rule_shelfSymmetry(Model, s):   # Break symmetry by ordering shelf sizes
    if s == Model.s.last():  # Skip for last shelf, since we're looking forward to the next shelf
        return pyo.Constraint.Skip
    else:
        return Model.ShelfHeights[s] >= Model.ShelfHeights[Model.s.next(s)]   # [Model.s.next(s)] is equivalent to [s + 1]
Model.shelfSymmetry = pyo.Constraint(Model.S, rule = rule_shelfSymmetry)

This constraint uses the Pyomo .next() function to represent the relationship between the current value of the s index and its next value. Conversely, the .prev() function represents the previous value in the set.

Importantly, a Pyomo Set (upper case "S") is ordered, unlike a regular Python set (lower case "s"). Having ordered sets allows us to represent relationships where order matters. A common application of ordered sets is time periods where, for example, we might want to model the change from one time period to the next.

Note that we need to Skip the last instance of this constraint, to avoid going past the end of the Set S. We do this by testing to see if the current value of s is the last() value of s in its Set.

Solver selection

Model 1 is non-linear, because we multiple variables in Equation (2). Non-linear models can be challenging to solve, especially at large scale. With our full data set of 20,000 pallets, this is quite a large model: Model 1 has 180,019 binary and integer variables, with a total of 540,070 non-zero values.

We tried different solvers on the 200 pallet test data, to see which ones perform well with Model 1:

Couenne. Fails to find a feasible solution in 1 hour.
Octeract on NEOS. Solves to optimality in 3 minutes.
BARON on NEOS. Solves to optimality in 18 seconds.
Gurobi. Solves to optimality in 2 seconds.

We can exclude Couenne from further use with Model 1.

Although Octeract is relatively slow, it is interesting because it explicitly reformulates Model 1 to be linear, then solves it using the HiGHS linear solver. Octeract/HiGHS is too slow for Model 1, but linearization is a potentially useful step, so we'll explore linearization of our model in the next article.

BARON and Gurobi look promising. BARON is a global solver, including mixed integer non-linearly constrained optimization problems. Gurobi's scope is narrower, but clearly it can quickly solve the type of quadratic problem that we have in Model 1 – at least for a small data set.

Model 1 solutions

A key question is how well Model 1 scales. It works OK for 200 pallets, but what about with more pallets?

Figure 7 shows objective function values and solve times for BARON and Gurobi using Model 1 and each of the data sets. That is:

200 pallets. Both BARON and Gurobi solve Model 1 to optimality in a few seconds, though Gurobi is significantly faster. The optimal solution has 8 racks, each of 7 shelves. This is a 20% reduction relative to the 10 racks needed to store for 200 pallets with our current warehouse design.
2,000 pallets. Both solvers take a few minutes to solve Model 1. The optimal solution has 74 racks, each of 7 shelves. This is a 26% reduction relative to the 100 racks needed to store 2,000 pallets with our current warehouse design.
20,000 pallets. Both solvers fail to find an optimal solution in 8 hours of running. BARON doesn't find any feasible solutions. Gurobi finds a feasible solution of 967 racks, each of 7 shelves – but this is only a 3.3% reduction relative to the 1,000 racks needed to store 20,000 pallets with our current warehouse design. Gurobi was converging very slowly, having improved the solution from 973.6 in the last hour.

Figure 7. Solver comparison for Model 1

The smaller data sets suggest that a significant reduction in the number of racks is possible. If we scale the solution of 74 racks for 2,000 pallets, then for 20,000 pallets there should be a solution with around 740 racks. That would be a great improvement. While this is promising, we're unable to solve Model 1 at full scale in a reasonable time.

Next steps: Linearize our model

Model 1 works for small data sets, but not for the full data set. This isn't surprising, as Model 1 with 20,000 pallets is quite a large non-linear model.

The Octeract solver reformulated our model to make it linear. Octeract doesn't say exactly how it did that, but there are techniques available for reformulating the multiplication of binary and integer variables, like we have in Equation (2). So, in the next article, we'll apply a linearization technique to make our model linear. We'll then see if we can solve a full data set to optimality in a reasonable time.

Conclusion

In this article, we develop a mixed integer non-linear program for designing shelves in a warehouse.

Model 1 works OK for small, test data. However, it fails to find a good solution for the full data set.

In the next article, we linearize our model, to see if it will perform better at a large scale.

If you would like to know more about this model, or you want help with your own models, then please contact us.

References

Cardona, L. F. & Gue, K. R. (2019). How to determine slot sizes in a unit-load warehouse, IISE Transactions, 51:4, pages 355-367.

Kevin Gue. (2019). Finding warehouse space in unexpected places.

Warehouse space for free: Non-linear model