23 July 2024

We continue our exploration of methods to solve our device rack positioning problem. The methods are:
- Model 1. Enumerate all possible position orders.
- Model 2. Search randomly for a specified time.
- Model 3. Constraint programming using OR-Tools.
- Model 4. Mixed integer linear programming using Pyomo.
The previous article describes Model 1, which uses enumeration of all possible permutations. That method works well for a small number of devices, up to about 12. But it fails to find good solutions for larger data sets because it takes too long to run – up to tens of billions of years, for the larger cases.
In this article, we develop Model 2, which tries a parallel random search method. The idea is to randomly generate possible solutions for a specified time, reporting the best solution we find. This method has an advantage over enumeration: it samples from all parts of the solution space, unlike Model's 1 enumeration method which is limited by run time to a specific part of the solution space. But will Model 2 perform better than Model 1?
30 June 2024

Most of the optimization models we work with involve finding the best combination of discrete decision variables. For example, allocating people to teams, designing warehouses, or scheduling staff.
A frequent question is, "Why not just look at all possible combinations and pick the best one?"
The answer is, sometimes, that's exactly what we do. In some situations, enumerating all feasible combinations of the variables is the easiest method for solving a problem.
But, in most situations, the number of combinations is too large. Many orders of magnitude too large. That's when we need more sophisticated methods, like mixed integer linear programming and constraint programming.
In this series of articles, we look at a simple situation that requires deciding the best order for positioning devices in a rack. We use four methods for solving this problem:
- Model 1. Enumerate all possible position orders.
- Model 2. Search randomly for a specified time.
- Model 3. Constraint programming using OR-Tools.
- Model 4. Mixed integer linear programming using Pyomo.
Along the way, we see how a problem's size can quickly escalate to a colossal magnitude. We also demonstrate how, contrary to popular belief, that magnitude is not necessarily a barrier to finding a good solution.
20 May 2024

When formulating an optimization model, a common question is "How do I express an IF function as a constraint?". Linear programs can't represent an IF function directly, so we need to use some linearization tricks to achieve the behaviour we want.
In previous articles, we've provided references to a variety of Transformation and linearization techniques, along with MIP formulations and linearizations. We've also described in detail how to formulate Logic conditions as constraints.
In this article, we examine the answers to a question on Operations Research Stack Exchange: Linear condition between two continuous variables. Specifically, the question asked:
There are two real variables \(x\) and \(y\). The conditions are such that:
\(\text{if } y \le 0, \text{then } x = 0\)
\(\text{if } y \gt 0, \text{then } x = y\)
How to write linear equations or inequalities to satisfy both the conditions?
Three answers are provided on Stack Exchange:
- Formulation 1. A special case method that has the advantage of being a pure linear program, though it works correctly only when the model has a specific form of objective function.
- Formulation 2. Uses a BigM approach that would normally work, but the answer has a subtle error.
- Formulation 3. Essentially the same as Formulation 2, except that it is correct.
We illustrate each of the methods both mathematically and graphically, to show how they are intended to mimic the required IF statements.
In addition, we derive a formulation from the more general situation for the constraint \(x = max(y, z)\).
18 April 2024

When doing analysis with an optimization model we commonly need to run many cases. For example, exploring a range of input value scenarios or evaluating a set of alternative designs.
In this article, we explore running optimization model cases in parallel. Specifically, we use the Python multiprocessing and mpi4py libraries to fully use the many CPU cores/threads in modern computers.
Our goals are to:
- Illustrate how to apply the multiprocessing and mpi4py libraries to running optimization model cases in parallel.
- Measure the performance of running cases in parallel compared with serially.
- Compare the performance of an old 4 core / 4 thread CPU with a new 20 core / 28 thread CPU, using the HiGHS solver.
As an example, we convert the serial model from a previous article, Warehouse space for free: Exogenous enumeration, to run multiple cases in parallel.
14 April 2024

Nathan Brixius has an interesting recent blog article about an old mixed integer programming (MIP) problem: Don Knuth’s MIP, 64 years later.
Don Knuth, a legendary computer scientist, wrote a paper in 1960 about optimizing computer performance, Minimizing drum latency time. Knuth formulated a MIP model, with 51 variables and 43 constraints. But he was unable to solve it after more than 10 hours of run time on an IBM 650 Data Processing Machine. One issue was that the machine had only 10 kB of memory. The model was eventually solved, 35 years later in 1995, using CPLEX and a more modern computer.
One issue was that the machine had only 10 kB of memory. The model was eventually solved, 35 years later in 1995, using CPLEX and a more modern computer.
Knuth describes the model, and its solution, in a note An integer programming problem unsolved for 35 years (in the "Unpublications" section).
Today, Knuth's formulation is a very small model. Demonstrating how much MIP solvers have improved over time, Nathan recreates the model and solves it with SCIP and Gurobi – each taking a fraction of a second to find an optimal solution.
This situation is reminiscent of our article Solver performance: 1989 vs 2024, in which we estimate how much the performance of MIP optimization solvers has improved over the last 35 years. Our analysis was prompted by a 1989 paper about an unsuccessful attempt to use MIP models to compile crossword puzzles. We have somewhat more success in our articles Crossword MILP - Model 1 and Crossword MILP - Model 2.
As Nathan says, the tremendous improvement in MIP solvers is another testament to the amazingly wonderful effectiveness of operations research!
27 March 2024

We conclude our project to improve the efficiency of a pallet warehouse by redesigning the warehouse's racks and shelves.
In part 2 of this article series, we linearized our warehouse racks and shelves design model with the hope of making it easier to solve at the full scale we need. It didn't work. Model 2 is even slower than the non-linear Model 1 we built in part 1.
In this article, we simplify our modelling by taking some of the variables out of the model and making them exogenous inputs. We enumerate all possible combinations of those exogenous inputs, then solve the simplified model for each combination. Hopefully, this time, our model will be solvable at the scale we need.
18 March 2024

In the first part of this article series, we formulated and implemented Model 1 for redesigning a pallet warehouse. Model 1, which in non-linear, works OK for small data sets, but it fails to find a good solution for the full data set.
In this article, we linearize our model using a standard technique. The idea is that, all going well, a linear model will be solvable at the scale we need.
11 March 2024

A common problem for warehouse managers is finding enough space to store everything:
We just don't have enough storage space. There used to be, but the company grew. Now, we have pallets stored in the dispatch area. They get in the way, and it's a health and safety hazard.
Warehouse Manager
In this article series, we look at improving the efficiency of a pallet warehouse (also known as a unit-load warehouse), where all items are stored on standard-size pallets.
Most pallet warehouses use a rack design where all shelves are the same size. This may not be the best design. Specifically, if the pallets have varying heights, then a single shelf height – designed to accommodate the tallest pallet – leaves unused space above some pallets. Depending on the mix of pallet heights, there's potentially a lot of unused space in aggregate.
To address this issue, we build a model of the warehouse's racks and shelves. Our objective is to find a design that minimizes the number of racks required to accommodate all pallets in the warehouse.
Along the way, we:
- Formulate a non-linear model of the situation.
- Compare several solvers, to see how they perform.
- Linearize our model to, hopefully, make it easier to solve.
- Disaggregate our model to make some variables exogenous, then iterate over an enumeration of the exogenous variables.
- Demonstrate use of Pyomo's
last()andnext()functions, which enable us to work with elements of ordered sets. - Turn off a constraint using Pyomo's
deactivate()function.
Importantly, we show that there's a surprising amount of extra storage space available for free, or minimal cost, just by redesigning the warehouse's racks and shelves.
13 February 2024
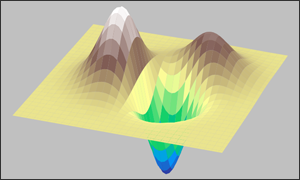
We're often asked questions about the seemingly odd behaviour of some models:
- Why does my model find different solutions each time I run it?
- The solver says the different solutions are all optimal. But some solutions are better than others. How can that be true?
- What can I do to make my model find the overall best solution?
In most cases, the answers are:
- The model is non-linear with multiple local optima. The solver may use a process that includes random elements that lead it to different neighbourhoods of the feasible region.
- Each solution is locally optimal, meaning that it is the best solution in that neighbourhood of the feasible region.
- To find the overall best solution, either use a solver than finds globally optimal solutions for that type of model, or solve the model multiple times, with different initial conditions, to make it more likely that the solver finds the best neighbourhood.
These answers generally require explanation, So, in this article, we explore some aspects of solver behaviour when solving non-linear optimization models. Our goal is to provide insights into what the solvers are doing, why they may find different solutions, and how we can improve our chances of finding at least a good, and hopefully a globally optimal, solution.
10 January 2024

In Part 1 of this series, we formulated a Mixed Integer Linear Program (MILP) for compiling crossword puzzles. Model 1 works OK, provided the crossword grid is small, not too dense, and the lexicon isn't too large. But as the grid gets denser and/or the lexicon gets larger, Model 1 struggles to find solutions.
We can do better. Model 1 uses a general formulation, where we specify the form of each constraint and then let the solver work out which variables and constraint instances aren't needed, given a specific data set. For many models, this approach is sufficient – largely because modern optimization solvers are very good at eliminating unnecessary terms in a model, especially in the presolve phase.
But solvers use general-purpose procedures for tightening models. Sometimes we can make use of our knowledge about the specific situation to help the solver.
In this article, we discuss techniques for fine-tuning the model-building process in Pyomo, to make a smaller and faster model. Specifically, we:
- Select only those words in the lexicon that fit in the current grid.
- Pre-populate some grid word slots with random words, to give the solver a head start.
- Omit constraint terms that don't meet some criteria.
- Skip some constraint instances entirely.
- Fix some binary variable values at zero, when we know they cannot have a value of one.
These steps tighten the model, making it easier for the solver to find a solution. We'll then look to solve larger crossword compilation problems.
