26 June 2021
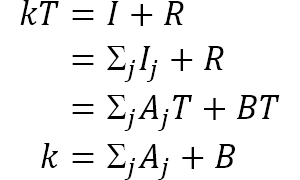
Punk Rock Operations Research has an interesting article about a 1967 paper On the art of modeling.
The paper's abstract says:
The problem of teaching or developing creative modeling ability is considered in the light of three basic hypotheses concerning the processes of enrichment (elaboration of very simple models), association (analogy with previously developed structures), and alternating attention to different aspects of the task.
Based on these hypotheses, specific steps are presented which have been developed to help individuals acquire modeling skills. The steps are illustrated by means of an example. Other sources of modeling ability are also suggested.
The discussion focuses on specific hypotheses concerning the differences between the teaching of models and the teaching of modeling.
Morris, W. T. (1967). "On the art of modelling"
The paper's insights and lessons are still highly relevant today, so it is definitely worth reading. We haven't found a freely available version of the paper, but it is available via ABI/INFORM or EBSCO which may be accessed through your local library web services.
17 May 2021

BCG Gamma have an interesting article that describes Five strategies for debugging MIP models.
There are many situations in which a MIP model must be debugged. The most common is when you run your model and get a message saying that it is infeasible or unbounded. Debugging can also be helpful when the model is feasible, but its solution does not behave as expected.
Five model debugging strategies:
- Inspect the .lp file. Mistakes in building the model can result in a failure to create the variables and constraints you intended. Review the .lp file to see what the solver is actually solving.
- Keep a small model instance. The .lp file size can grow very quickly. To keep the file readable, make toy models that are small enough that you can inspect the file while not being so simplistic that you lose important aspects of the real-sized model.
- Selectively remove families of constraints. The idea is to find a smaller, but still infeasible, version of your model. This allows you to identify which groups of constraints are causing infeasibility.
- Compute the irreducible inconsistent subsystem (IIS). Some solvers have an automatic method for computing which constraints cause infeasibility. The product is the smallest subset of constraints causing your model to be infeasible. Fixing the infeasibility is still a manual process.
- Use penalized artificial variables to relax constraints. An artificial variable allows a constraint to be violated, if necessary, at a cost. The relaxed system of inequalities will always have a solution, enabling you to identify which constraints are causing infeasibility.
These strategies can be combined to help you debug your model.
3 May 2021

In this article we replicate an academic paper's model formulation of a COVID-19 vaccination plan for Hong Kong.
The model represents the supply of, and demand for, vaccine doses as a transportation problem, with doses "transported" from month-to-month given a storage cost rate. The objective is to minimize the total storage cost, while matching monthly supply and demand.
The paper's author solves the model using Excel and Solver. We do the same, though we also use OpenSolver – to see how it behaves differently. To incentivize the model to produce an intuitively better solution, we extend the model to include an escalating cost over time.
20 April 2021
Yet Another Math Programming Consultant (YAMPC) has a couple of interesting articles exploring different model formulations for machine scheduling problems:
- Parallel machine scheduling I, two formulations.
- Parallel machine scheduling II, three more formulations.
The situation involves scheduling 50 jobs on 4 parallel machines, with precedence relationships between jobs and multiple weighted objectives.
Five different formulations are analyzed:
- Model 1. Jobs are scheduled in discrete time slots.
- Model 2. Jobs are scheduled in continuous time.
- Model 3. A variation of Model 1.
- Model 4. A more complex variation of Model 2.
- Model 5. A positional, rather than time-based, model.
In this situation, Model 1 is the simplest and it performs the best – by a substantial margin.
YAMPC concludes that choosing the right formulation can pay off (though often we need to do numerical tests to determine which formulation is best), and having different formulations is an excellent debugging tool as they give us confidence that the results are correct.
17 April 2021

Allocating people to teams is a common task in both sport and business. Often we want the teams to be as balanced as possible. But making the allocation can be a difficult problem, especially if there are many people or we need to form several teams.
In this article we build and analyze a model that allocates 32 people to four teams, with the objective of each team having an aggregate rating that is as balanced as possible. The task is complicated by having three types of position in the teams, with a diversity of ratings across the available people.
The model is built in Excel and solved using either Solver or OpenSolver.
5 April 2021
To learn about optimization modelling, the Optimization 101 website is a great place to start.
The website aims to provide "a complete but compact introduction to the major topics in optimization". The content is divided into chapters, like a book, covering topics that include:
- Linear Programming.
- Sensitivity Analysis.
- Networks.
- PERT for Project Planning and Scheduling.
- Integer / Discrete Programming.
- Binary and Mixed-Integer Programming.
- Dynamic Programming.
- Nonlinear Programming (NLP).
1 April 2021
The BBC has an interesting article: Do 'maximisers' or 'satisficers' make better decisions?
According to the article, there are two main types of decision-makers:
- 'Maximizers' weigh choices carefully to assess which is the best one.
- 'Satisficers' make decisions quickly and accept a 'good enough' outcome.
Each approach comes with benefits and drawbacks. Being a maximizer tends to be very time-consuming and can lead to post-decision regret and counterfactual thinking. Conversely, satisficers may not necessarily get the best outcome. As a general rule, maximizers do better but feel worse.
Of course, at SolverMax we focus on optimization modelling, so obviously we prefer the maximizer approach. But even then, often it can take a solver a very long time to find an optimal solution. In such situations we may have to accept a near-optimal solution as the best practical trade-off between outcome and timeliness.
As the article suggests, perhaps the best way to make decisions may be by combining maximizer and satisficer tendencies.
29 March 2021
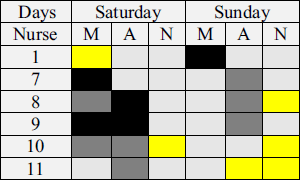
The Nurse Scheduling Problem (NSP) is a well-known optimization situation. The objective is to find an optimal way to assign nurses to shifts, where each nurse has their preferences for which shifts they would like to work. In addition, we need to meet the operational needs of the hospital in terms of nurse numbers and attributes for each shift.
Of course, a model of the NSP can be applied to constrained scheduling problems in many other situations.
A paper published in December 2018 describes a new formulation and solution for the Nurse Scheduling Problem, along with a real case study of applying the model in an Egyptian hospital.
The authors claim that the model improves the level of nurses’ satisfaction by considering their preferences, as well as decreasing the overall overtime cost by 36%.
A PDF of the paper is available at: A new formulation and solution for the nurse scheduling problem: A case study in Egypt.
24 March 2021

A recent project involved fixing a Solver model. The model was intended to be a straightforward Linear Program to find the optimal mix of three chemicals, subject to the proportions of the chemicals being within specific bounds.
That is, the model had constraints like: \({a \over a+b+c} \le p_a\)
where \(a\), \(b\), and \(c\) are variables for the quantity of each chemical, and \(p_a\) is a constant representing the upper bound on the proportion for chemical \(a\).
The problem was that this constraint is non-linear because a variable is divided by other variables. It may also cause a division by zero error. Solver's non-linear and evolutionary methods didn't always work well with this model.
Fortunately, we can rearrange the constraint to be in an equivalent linear form. That is: \({a \times (1 - p_a) \le p_a \times (b + c)}\)
With this reformulation, the model becomes linear while still achieving the desired intent. Consequently, the model now solves to optimality quickly and reliably using the Simplex method.
15 March 2021
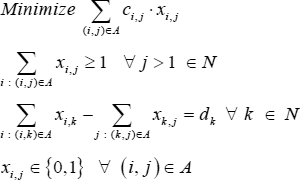
Designing an optimization model can be difficult. In seeking guidance, we often look for inspiration from the published academic literature. Since the 1950s, there has been an enormous amount of research into how to design and solve optimization models for a wide range of situations, with models for just about anything we could want.
There is much that we can learn from the literature, if only we could understand it. Many academic papers include a statement of the model's design, known as the formulation, using mathematical notation that can look impenetrable. The notation is seldom explained, so translating a formulation into a working model can be a perplexing and frustrating process.
But with a little knowledge about what the notation means, we can gain a lot of insight into how to design or improve our models. The purpose of this article is to explain the meaning of common mathematical notation and illustrate how we can apply the knowledge contained in academic papers to help us build working models in Excel.
