1 April 2021
The BBC has an interesting article: Do 'maximisers' or 'satisficers' make better decisions?
According to the article, there are two main types of decision-makers:
- 'Maximizers' weigh choices carefully to assess which is the best one.
- 'Satisficers' make decisions quickly and accept a 'good enough' outcome.
Each approach comes with benefits and drawbacks. Being a maximizer tends to be very time-consuming and can lead to post-decision regret and counterfactual thinking. Conversely, satisficers may not necessarily get the best outcome. As a general rule, maximizers do better but feel worse.
Of course, at SolverMax we focus on optimization modelling, so obviously we prefer the maximizer approach. But even then, often it can take a solver a very long time to find an optimal solution. In such situations we may have to accept a near-optimal solution as the best practical trade-off between outcome and timeliness.
As the article suggests, perhaps the best way to make decisions may be by combining maximizer and satisficer tendencies.
29 March 2021
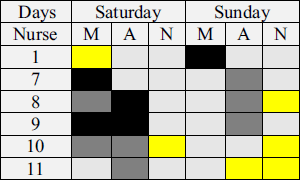
The Nurse Scheduling Problem (NSP) is a well-known optimization situation. The objective is to find an optimal way to assign nurses to shifts, where each nurse has their preferences for which shifts they would like to work. In addition, we need to meet the operational needs of the hospital in terms of nurse numbers and attributes for each shift.
Of course, a model of the NSP can be applied to constrained scheduling problems in many other situations.
A paper published in December 2018 describes a new formulation and solution for the Nurse Scheduling Problem, along with a real case study of applying the model in an Egyptian hospital.
The authors claim that the model improves the level of nurses’ satisfaction by considering their preferences, as well as decreasing the overall overtime cost by 36%.
A PDF of the paper is available at: A new formulation and solution for the nurse scheduling problem: A case study in Egypt.
24 March 2021

A recent project involved fixing a Solver model. The model was intended to be a straightforward Linear Program to find the optimal mix of three chemicals, subject to the proportions of the chemicals being within specific bounds.
That is, the model had constraints like: \({a \over a+b+c} \le p_a\)
where \(a\), \(b\), and \(c\) are variables for the quantity of each chemical, and \(p_a\) is a constant representing the upper bound on the proportion for chemical \(a\).
The problem was that this constraint is non-linear because a variable is divided by other variables. It may also cause a division by zero error. Solver's non-linear and evolutionary methods didn't always work well with this model.
Fortunately, we can rearrange the constraint to be in an equivalent linear form. That is: \({a \times (1 - p_a) \le p_a \times (b + c)}\)
With this reformulation, the model becomes linear while still achieving the desired intent. Consequently, the model now solves to optimality quickly and reliably using the Simplex method.
15 March 2021
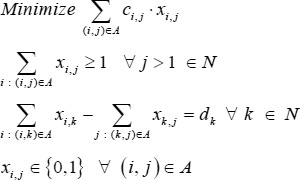
Designing an optimization model can be difficult. In seeking guidance, we often look for inspiration from the published academic literature. Since the 1950s, there has been an enormous amount of research into how to design and solve optimization models for a wide range of situations, with models for just about anything we could want.
There is much that we can learn from the literature, if only we could understand it. Many academic papers include a statement of the model's design, known as the formulation, using mathematical notation that can look impenetrable. The notation is seldom explained, so translating a formulation into a working model can be a perplexing and frustrating process.
But with a little knowledge about what the notation means, we can gain a lot of insight into how to design or improve our models. The purpose of this article is to explain the meaning of common mathematical notation and illustrate how we can apply the knowledge contained in academic papers to help us build working models in Excel.
1 March 2021

"Job sequencing" is a common management problem, especially in manufacturing and production businesses.
That is, given a set of jobs, what is the job sequence that takes the minimum total time?
The benefits from improved sequencing can be substantial, while a poor sequencing solution can be expensive. To illustrate how an optimization model can help us make the decision, in this article we solve a simple job sequencing problem using Solver.
22 February 2021

"Fantasy sports" is a popular pastime. Like in many real sports, the performance of a fantasy sports team may be determined by relatively small margins. The selection of a slightly better team can lead to substantially better performance.
To help achieve better team performance, we explore a team selection optimization model built in Excel and solved with OpenSolver.
15 February 2021

"Wire cutting" is a common type of production problem. That is, given available stock of wire (or other one-dimensional stock material) and a list of pieces required, what is the best way to cut the stock to fulfil the requirements while minimizing waste?
The benefits from improved cutting can be substantial, while poor cutting choices can be expensive. To illustrate how an optimization model can help us make the decision, in this article we design, build, and solve a wire cutting problem using OpenSolver.
8 February 2021

"Production mix" planning is a common business problem. That is, given available resources, what mix of products should we make to maximize profit?
With potentially many trade-offs between production choices and available resources, deciding on the best volume for each product can be a complex decision. The gains from making a better decision can be substantial, leading to improved profit and more efficient use of resources.
25 January 2021

The "facility location problem" is a common, and often difficult, decision that organizations need to make.
Facilities may include assets such as factories, warehouses, shops, mobile telephone sites, etc. Such assets are typically long-lived, so the decision about where to build them has a long-term impact on the organization.
A wrong, or sub-optimal, decision is likely to be very expensive. To help make the decision, we can model the facility location problem using an optimization model in Excel.
11 January 2021
This is a blog about optimization modelling.
We focus on building optimization models in either Python (using a variety of libraries, such as Pyomo and OR-Tools) or Excel (using the Solver or OpenSolver add-ins).
Topics include:
- Optimization model examples, with detailed explanations and Excel spreadsheets available for download.
- Projects we've worked on recently (anonymized, of course).
- Links to posts by other optimization bloggers.
- Interesting developments in the optimization field.
- Updates to relevant software.
- Anything else relating to optimization modelling that grabs our attention.
If you want help with your own models, or if you would like to know more about anything mentioned in this blog, then please contact us. To support the creation of new content, please buy us a coffee.
