Solver Max - Fantasy sports: Pick the best team

22 February 2021

"Fantasy sports" is a popular pastime. Like in many real sports, the performance of a fantasy sports team may be determined by relatively small margins. The selection of a slightly better team can lead to substantially better performance.

To help achieve better team performance, we explore a team selection optimization model built in Excel and solved with OpenSolver.

Download the models

The model is available on GitHub.

Situation

In a fantasy sport, participants select a virtual team composed of proxies for real professional players. The virtual teams compete based on the performance of the selected players in actual games. In some fantasy sport games, prizes are awarded to the best-performing virtual teams.

The rules of a fantasy sports game vary from sport to sport and depend on the game organizer. In this example, let's assume the following rules:

We have a list of 100 available players.
A team consists of 11 players.
Each player has a price and a points value (which indicates their quality, higher being better).
The players are ranked according to their points value.
The team is divided into six positions (designated as GK, BK, DP, MF, AF, and ST). The meaning of the positions is not important for this model.
Each player is available for a specific position.
The number of players in each position must be at least a specified minimum and no more than a specified maximum.
The total price of the selected players must not exceed the specified team budget, for example, $80,000.

Model design

Potential modelling approaches

This is a classic binary choice situation, where each player is either selected for the team, or not.

Our objective is to select the best team. We interpret that objective to mean the team with the highest total points value – though other interpretations are possible.

The model must comply with the rules of the game. In addition, we'll find it useful to include assumptions and/or constraints that allow us to explore the potential solutions beyond a simple optimal solution.

Player data

Player list — Figure 1. Part of the player list

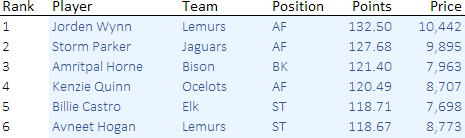
Figure 1 shows the data for the first few available players. For each player, the list shows:

Rank, in terms of points.
Player name.
The player's team. We don't use this column in our model, though some game rules limit the number of players that may be selected from a team.
The position of the player.
Points that the player has.
The player's price.

It is useful to see how the player points and price are related, so we plot those values for all 100 players in Figure 2. The chart also highlights the points that represent the players selected in a solution.

Reflecting a relationship that often occurs with elite sports people, better players have increasingly higher prices. In this example, the two best players, as measured by the points system, have prices that are significantly higher than any other player. There's also significant variation in price for similar points value, reflecting the fact that the points system is an imperfect representation of a player's value.

Figure 2. Relationship between player points and price

Distribution of potential team point totals

Before we look at our optimization model, it is instructive to look at the distribution of potential team point totals:

Across the 100 available players, their points average 63.74.
Therefore, ignoring all other constraints, a team of 11 players would have an average total of around 700 points (approximately = 63.74 * 11).
The top ranked 11 players have a total of 1,294.61 points. However, their total price exceeds the budget and a team comprised of those players does not meet the position requirements. Therefore, such a team is infeasible.
Similarly, the lowest ranked 11 players have a total of 262.30 points. Though their total price is OK, a team comprised of those players does not meet the position requirements. Again, such a team is infeasible.

This analysis suggests a wide distribution of possible solutions. To explore the solutions, we randomly generated 10,000 feasible solutions. The distribution of total team points from those solutions is shown in Figure 3.

The average total team points from this sample is 693.56 (very close to the 700 mentioned above), and the maximum is 1,015.74 points.

It is possible that higher point totals exist, though very high totals are rare. Only 8 of the 10,000 solution have total team points of between 976 and 1000, and a further 4 of the solutions have total points in excess of 1,000.

Figure 3. Distribution of 10,000 random, feasible solutions

Model formulation

The mathematical formulation of our model is shown in Figure 4.

That is:

Equation (1). We want to maximize the player points across the selected team.
Equation (2). By selecting candidate players below a specified rank (lower rank is better).
Equation (3). The number of selected players must equal the team size.
Equation (4). There is an upper bound on the number of selected players in each position.
Equation (5). There is a lower bound on the number of selected players in each position.
Equation (6). The price of selected players must be within the budget.
Equation (7). We may specify that some players must be selected.
Equation (8). A candidate player is either selected or not.

Figure 4. Mathematical formulation

\begin{alignat*}{1} &\text{Objective} \\ & \quad \text{Max } fPointsTeam \ &= &\quad \sum_{c=1}^n \left( \text{dPoints}_{c} \times vSelection_{c} \right) \tag{1} \\ \\ &\text{Subject to} \\ & \quad \text{dPlayerRankMax} &\ge &\quad \text{dRank}_{c} \times vSelection_{c} \quad &\forall \ c \in C \tag{2}\\ & \quad \text{dTeamSize} \quad &= &\quad \sum_{p=1}^m \sum_{c=1}^n \big( \left( \text{dPosition}_{c} = p \right) \times vSelection_{c} \big) \tag{3} \\ & \quad \text{dPositionMax} &\ge &\quad \sum_{c=1}^n \big( \left( \text{dPosition}_{c} = p \right) \times vSelection_{c} \big) \quad &\forall \ p \in P \tag{4}\\ & \quad \text{dPositionMin} &\le &\quad \sum_{c=1}^n \big( \left( \text{dPosition}_{c} = p \right) \times vSelection_{c} \big) \quad &\forall \ p \in P \tag{5}\\ & \quad \text{dBudget} &\ge &\quad \sum_{c=1}^n \left( \text{dPrice}_{c} \times vSelection_{c} \right) \tag{6} \\ & \quad vSelection_{c} &\ge &\quad \text{dSelectionRequire}_{c} \quad &\forall \ c \in C \tag{7}\\ \\ &\text{Variables} \\ & \quad vSelection_{c} &= & \quad\begin{cases} 1, &\text{if candidate $c$ is selected} \\ 0, &\text{otherwise} \tag{8} \end{cases} \quad \quad &\forall \ c \in C \\ \\ &\text{Data} \\ & \quad \text{dBudget} &= &\quad \text{Positive real, \$} \tag{9} \\ & \quad \text{dTeamSize} &= &\quad \text{Positive integer} \tag{10} \\ & \quad \text{dPlayerRankMax} &= &\quad \text{Positive integer} \tag{11} \\ & \quad \text{dRank}_{c} &= &\quad \text{Positive integer} \quad &\forall \ c \in C \tag{12}\\ & \quad \text{dPoints}_{c} &= &\quad \text{Positive real} \quad &\forall \ c \in C \tag{13}\\ & \quad \text{dPrice}_{c} &= &\quad \text{Positive real, \$} \quad &\forall \ c \in C \tag{14}\\ & \quad \text{dPosition}_{c} &= &\quad \text{Text} \quad &\forall \ c \in C \tag{15}\\ & \quad \text{dPositionMin}_{p} &= &\quad \text{Positive integer} \quad &\forall \ p \in P \tag{16}\\ & \quad \text{dPositionMax}_{p} &= &\quad \text{Positive integer} \quad &\forall \ p \in P \tag{17}\\ & \quad \text{dSelectionRequire}_{c} &= &\quad\begin{cases} 1, &\text{if candidate $c$ is required} \\ 0, &\text{otherwise} \tag{18} \end{cases} \quad &\forall \ c \in C \\ \\ &\text{Sets} \\ & \quad C &\ &\quad \text{Candidate player} \tag{19} \\ & \quad P &\ &\quad \text{Team position} \tag{20} \\ \\ &\text{Dimensions} \\ & \quad m &\ &\quad \text{Number of candidates} \tag{21} \\ & \quad n &\ &\quad \text{Number of position types} \tag{22} \\ \\ &\text{Bounds} \\ & \quad \text{Non-negative} &\ &\quad \tag{23} \\ \end{alignat*}

Implementation

Specify the position requirements

For the six types of position in the team, the game specifies requirements for lower and upper bounds on the number of players who may be selected – as shown in Figure 5.

The GK position has lower and upper bounds of 1, meaning that there must be exactly one player in that type of position. The BK position has a lower bound of 1 and an upper bound of 3, meaning that the model may select 1, 2, or 3 players in that type of position.

Note that the number of players in a team must be within the total position bounds. Given this data, the team size must be between 8 and 16, inclusive. Our team size is specified as 11, which is OK.

Solver model

Objective function

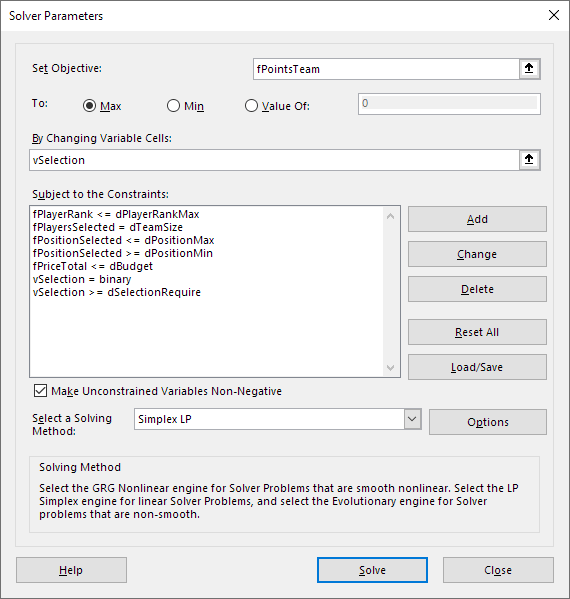
The Solver model is shown in Figure 6. Our objective is to maximize fPointsTeam, the total number of points for the selected players.

Variables

The model has just one set of variables:

vSelection. A binary variable for each player, indicating whether they have been selected to be in the team.

Constraints

The constraints are:

fPlayerRank <= dPlayerRankMax. An optional constraint to limit the maximum player rank. Set to 100 to have no effect.
fPlayersSelected = dTeamSize. The number of selected players must equal the required team size.
fPositionSelected <= dPositionMax. The number of players in each type of position must be no more than the specified maximum.
fPositionSelected >= dPositionMin. The number of players in each type of position must be at least the specified minimum.
fPriceTotal <= dBudget. The total price of the selected players must be no more than the specified team budget.
vSelection = binary. The selection variables are binary.
vSelection >= dSelectionRequire. An optional constraint to require some players to be selected. Set value to 1 to require selection. Use carefully, as it is easy to make the model infeasible.

Solution method

This is a Mixed Integer Program (MIP), so it can be solved efficiently using the Simplex method.

The model is too large for Solver, so OpenSolver is required. An optimal solution is found in a few seconds.

Analysis

Optimal solution

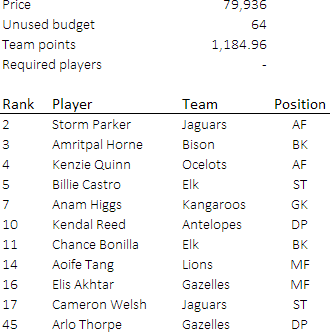
The optimal solution, which we'll call Scenario A, is shown in Figure 7. This solution does not use either of the optional constraints.

Key points to note:

Total team points equal 1,184.96, which is substantially better than the best random solution shown in Figure 3.
The model used almost all the budget, leaving just 0.08% unused.
Six of the top ten ranked players are selected, though the player ranked #1 is not selected.
The lowest-ranked player is #45. This is lower than most people would select manually, though this player's points value is close to the average of the 100 available players.

Alternative solutions

The Scenario A solution looks like an excellent team. However, we might be uncomfortable with the selection of the #45th ranked player. So, we can explore alternative solutions by using the optional maximum rank and required player constraints.

Selecting some values for those constraints leads to the following scenarios:

Scenario A: Maximum rank 100, no required players. Points = 1,184.96. Doesn't select rank #1. Lowest rank is #45.
Scenario B: Maximum rank 30, no required players. Points = 1,183.00. Doesn't select rank #1 or #2. Lowest rank is #26.
Scenario C: Maximum rank 100, require players rank #1 and #2. Points = 1,171.90. Lowest rank is #50.
Scenario D: Maximum rank 30, require players rank #1 and #2. Points = 1,153.72. Lowest rank is #30.

These scenarios illustrate some of the trade-offs that need to be made when selecting a fantasy sports team. Selecting high-ranked players will typically force the inclusion of lower-ranked players, so that we can stay within the budget constraint. This may reduce the overall points value of the team.

If we try to constrain the model too much, then it is likely that we'll make the model infeasible. For example, if we set the maximum rank to 25, then there is no feasible combination of the player position constraints within the given team budget. If we had a larger budget, then a team is possible – but with a budget of $80,000 it is not.

It is a judgement call as to whether any of the alternative scenarios are preferred over Scenario A. In particular, Scenario B might be attractive, as it avoids the player with a rank of #45, with only a small reduction in total points for the team – though it doesn't select either of the two highest-ranked players. Conversely, requiring the players ranked #1 and #2 significantly reduces the total team points, due to the relatively high price of those two players using so much of our limited budget.

Many other alternative scenarios are possible. The art of playing fantasy sports is making judgements about subtle trade-offs between the various attributes of the team, informed by an optimization model such as this one.

Optimal points given a range of budgets

Finally, it is likely that the game organizers set the team budget at a level that constrains the player selection choices, to make the game more interesting.

In this example, the game organizers set the budget at $80,000. To see the effect of the budget constraint, Figure 8 shows the optimal points for budgets that vary from $60,000 to $100,000.

The optimal team points increase until the budget reaches $89,554. Above that amount, the budget constraint is no longer binding. Instead, the solutions are constrained by the available players and the position constraints, leading to a constant optimal objective function value of 1,253.81 points.

Figure 8. Optimal team points given a range of budgets

Conclusion

This model is an example of selecting an optimal fantasy sports team in Excel.

Using an optimization model to pick a fantasy sports team doesn't guarantee success, but it does improve the odds.

If you would like to know more about this model, or you want help with your own models, then please contact us.

Fantasy sports: Pick the best team