7 March 2022
Attached is a free, 681 page textbook: Decision Modeling. The textbook is written by David M. Tulett, Associate Professor in the Faculty of Business Administration at Memorial University in Canada.
Topics covered by the textbook include: optimization of linear, integer, and nonlinear models, as well as the use of decision trees. Both Excel Solver and LINGO are used extensively to build and solve the many example models.
According to the Introduction:
Decision Modeling involves the creation of mathematical models which represent problems faced by business management. To a lesser extent, it also involves numerically solving these models. ...
If there's a difficulty with this subject, it's probably not the mathematics. Instead, the difficulty is likely to be the building of the model which the mathematics seeks to solve. The important thing is always going from a problem description to a model for the problem.
Tulett, D. M. (2022). "Decision Modeling"
Download the full textbook as a PDF (version 3.0.4, 3 March 2022): Decision Modeling ![]()
Updates for the textbook are available from Linney, Memorial University's Centre for Innovation in Teaching and Learning (CITL).
5 March 2022
Professor Rubin recently posted an article about finding all solutions to a network model: Finding almost all paths. The article mentions two techniques that we explored in our article Taking a dip in the MIP solution pool. Specifically, Professor Rubin says:
To find all solutions, one possible approach is to solve whatever MIP model you choose, then add a "no-good" constraint that eliminates the solution just found (and only that one) and solve again, until eventually the aggregation of "no-good" constraints makes the model infeasible. What I did instead was to use the "populate" command in CPLEX, which accumulates a pool of solutions.
An issue with the CPLEX solution pool is that it isn't guaranteed to find all optimal solutions. So, the Professor also describes a brute force method to find all solutions. The article presents analysis that demonstrates that the brute force performs better in this case – that is, the brute force method is both faster and more reliably finds all solutions.
Although clever solvers are often the best method we have, it is good to remember that brute force can be a useful – and sometimes efficient – method for solving a problem. We used a brute force method for the situation described in our article Job sequencing to minimize completion time. In that situation, brute force enumeration was very effective for small data sets, though it quickly became impractical for large data sets.
In summary, we can extend our list of techniques for finding all solutions to include:
- CPLEX solution pool.
- Eliminate known solutions.
- Brute force enumeration.
If you know of any other methods for finding all (or almost all) solutions to an optimization problem, or you want help with your own models, then please contact us.
21 February 2022

We're frequently asked questions like: "How many other optimal solutions exist?" and "How do I find those solutions?". Often these questions are prompted by our mentioning that most models have alternative optima – that is, optimal solutions with the same objective function value, but different variable values.
Although a model may have a unique optimal solution, models with integer/binary variables typically have multiple optimal solutions, and continuous linear models may have an infinite number of alternative optimal solutions. The likely existence of multiple alternative optima is why we usually say "an optimal solution", rather than saying "the optimal solution".
Sometimes people also ask, "How do I find solutions that are almost optimal?". This question typically indicates that the decision maker may accept a sub-optimal solution (or an alternative optimal solution) that is "better" according to some criteria that aren't captured by the model design. Of course, we should look at incorporating the unspecified criteria within the model, but sometimes that is difficult or even impossible. In any case, exploring the solution space around the optimal solution is an important part of the modelling process.
This article describes methods for finding alternative optima and solutions that are almost optimal. Specifically, we explore the CPLEX "solution pool" feature, which NEOS Server has recently made available through their online portal.
29 January 2022

When formulating a model, many of the problems we encounter involve non-linear formulae. For example, a fixed cost is incurred only if a facility is built, or a variable can take values only in the ranges 5 to 10 or 80 to 100.
Optimization models work best when the objective function and constraints are all linear. In some situations, it is possible to reformulate a model to linearize the non-linear parts. The techniques for linearizing non-linear formulae can make the difference between a model being viable or not.
FICO Xpress Optimization have written a booklet that describes a variety of useful mixed-integer programming (MIP) formulations and linearizations, including:
- Binary variable logical conditions.
- Minimum, maximum, and absolute value of binary variables.
- Multiplication of variables.
- Variables with disjunctions.
- Batch sizes.
- Minimum activity level.
The booklet is available at: MIP formulations and linearizations.
17 December 2021

The COIN-OR Foundation is seeking support to continue providing open-source optimization software for the operations research community. They have published an article, Future of COIN-OR, describing their challenges in securing funding and the participation of community members to continue operating.
COIN-OR are responsible for the development of more than 70 projects that are widely used in optimization tools, including:
- Pyomo, a Python-based optimization modeling language.
- PuLP, a Python library for linear optimization.
- CBC, the default mixed integer linear programming solver used in OpenSolver and elsewhere.
- Bonmin and Couenne, non-linear mixed integer programming solvers.
The COIN-OR Foundation presents three possible future directions:
Option 1: Wind down the COIN-OR Foundation activities related to maintenance and development of common infrastructure and existing codes that are not otherwise maintained.
Option 2: Continue operating in a haphazard fashion and hope that the community will eventually take up the cause as things slowly degrade.
Option 3: Find a path to funding the current activities of the COIN-OR Foundation in a sustainable way.
To achieve Option 3, the Foundation needs your support. You can either donate to COIN-OR, or email them at
2 December 2021

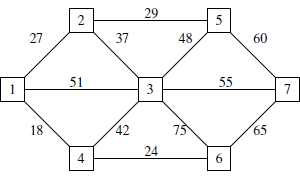
Project crashing is the process of compressing a project plan by using additional resources to reduce the duration of some tasks.
Using additional resources incurs additional cost, so it is important that the resources are deployed to the tasks that produce the greatest benefit. A project manager must decide an appropriate trade-off between time and cost for each task, leading to the best revised project plan. Given the dependencies between project tasks, making these trade-offs can be complex and difficult, even for a small project.
This article describes an example of project crashing using an optimization model to help the project manager decide what to do.
16 November 2021

Recently we were working on a small one-dimensional bin packing model. The situation was simple, and we expected the model to be easy to solve. But there was just one problem: we couldn't find an optimal solution, even after letting the solver run overnight for 12 hours.
Initially, we were using the CBC solver. Since that didn't work, we tried CPLEX via NEOS, but we encountered the same problem – CPLEX couldn't find an optimal solution either.
So, we searched the Operations Research literature for an alternative formulation. We discovered a recently published academic paper that has a new, innovative formulation for one-dimensional bin packing (and potentially other types of packing situations).
This article describes the new formulation and our experience applying it to our simple, yet difficult to solve, model.
5 November 2021
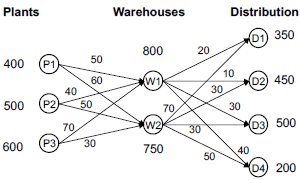
There are many tools for building an optimization model, including:
- Excel/OpenSolver, which provides a familiar, interactive, visual grid for modelling.
- Python, plus the CVXPY or PuLP library, which provides a programmatic way to define a model.
Each tool has advantages and disadvantages, as we discussed in Optimization in Excel vs Python.
The tool CMPL (<Coliop|Coin> Mathematical Programming Language) occupies an intermediate position. That is, CMPL combines the advantages of working with the data and solution in Excel, while providing the power and flexibility of a programming language for defining the model.
According to the tool's website:
The CMPL syntax is similar in formulation to the original mathematical model but also includes syntactic elements from modern programming languages. CMPL is intended to combine the clarity of mathematical models with the flexibility of programming languages.
Steglich, M. (2021). "Optimisation Modelling with Excel and CMPL2"
CMPL has recently been updated to version 2.0, as described in the paper "Optimisation modelling with Excel and CMPL2". The paper provides a good overview of CMPL, including a couple of examples to help you get started*.
* Note that there's a bug in the paper's transhipment example. You'll need to add minCap[edges] to the definition in line 01 of Listing 7.
7 October 2021
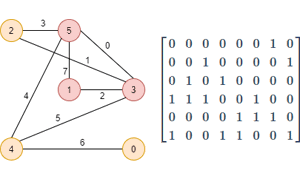
Vamshi Jandhyala has an interesting series of blog posts about Optimization using linear models.
Each article includes a description of the topic, along with several examples written in Python and solved using the Gurobi commercial solver:
- Modeling using Linear Programming. Illustrates some concepts of linear programming via the formulation and solution of a resource allocation problem.
- Modeling using Integer Programming. Describes several applications of integer programming, including an assignment problem, graph coloring, the 0-1 knapsack problem, a set covering problem, and a class scheduling example.
- Graphs and Integer Programming. Explores some graph theory applications of integer programming, including finding a maximal independent set and finding the maximal clique of a set.
The examples include Python source code, though they are sufficiently small that they could be translated to use your preferred modelling tool and solver.
3 October 2021

OpenSolver uses the free, open-source CBC solver. For most linear models, CBC is good enough. But sometimes CBC struggles to solve a model in a reasonable time. That usually happens when the model has a large number of variables or constraints, though some small models can also be difficult to solve.
When CBC doesn't get the job done, we can try using a more powerful solver. One way to apply more power is to use the NEOS Server, which is an online service that provides access to many different solvers, including commercial solvers, for free.
This article describes an example of how we can solve a model using the CPLEX solver via the NEOS Server.
