8 February 2021

"Production mix" planning is a common business problem. That is, given available resources, what mix of products should we make to maximize profit?
With potentially many trade-offs between production choices and available resources, deciding on the best volume for each product can be a complex decision. The gains from making a better decision can be substantial, leading to improved profit and more efficient use of resources.
Download the model
The model is available on GitHub.
Situation
You own a boutique pottery business, making and selling two types of large ornamental products called Lunar Orb and Solar Disc.
Your current production involves:
- 8 full-time team members, who each work 40 hours per week for a total of 8 * 40 = 320 person-hours/week. Allowing for holidays, training and other activities, your team collectively has a total of 250 person-hours per week available for production.
- Each Lunar Orb takes 10.0 person-hours to make, while a Solar Disc takes 12.5 person-hours.
- Allowing for wastage, each Lunar Orb uses 30kg of materials (mostly clay), while a Solar Disc uses 18kg of materials.
- You have a standing order for 500kg of materials, which is received early every Monday.
- Lunar Orbs tend to sell better than Solar Discs, so that you often run out of Lunar Orbs to sell. Experience suggests that you can sell no more than twice as many Lunar Orbs as Solar Discs, because most people buy either an individual Lunar Orb or a combination of Lunar Orb plus Solar Disc.
- Currently you’re producing, on average, 7.5 Lunar Orbs and 14.0 Solar Discs each week.
- Your current production volume was chosen to keep your team busy. i.e. 10.0 person-hours per Lunar Orb * 7.5 Lunar Orbs per week + 12.5 person-hours per Solar Disc * 14.0 Solar Discs per week = 250 person-hours/week.
- You aim to sell all your production each week, holding no inventory of finished products.
- Taking into account the cost of materials, wages, packaging, and other production costs, your gross profit is $200 for each Lunar Orb and $80 for each Solar Disc. From the gross profit you need to pay other costs, like rent, that are not a function of production volume.
- Given the current production mix, your total gross profit is $2,620 per week. i.e. $200 per Lunar Orb * 7.5 Lunar Orbs per week + $80 per Solar Disc * 14.0 Solar Discs per week = $2,620 per week.
You’re not using all the 500kg order of materials available per week. That is, 30kg per Lunar Orb * 7.5 Lunar Orbs per week + 18kg per Solar Disc * 14 Solar Discs per week = 477kg/week. Because you have materials left over, you’re planning to reduce your standing order for materials.
Model design
The solution space
Your objective is to maximize gross profit per week. The gross profit is limited by the constraints described above. We need to decide the number of Lunar Orbs and Solar Discs to produce each week.
Since you produce only two products, we can represent the potential range of production volume of each product using a 2D chart. This chart illustrates what is known as the "solution space".
Figure 1 shows the solution space for your production mix problem. We plot the production of Solar Discs on the x-axis and the production of Lunar Orbs on the y-axis. Any combination of production of the two products represents a potential solution to the problem.
The red line of the chart represents the "People" constraint. That is:
- Your team has 250 person-hours available for production each week.
- A Lunar Orb takes 10.0 person-hours to make, so if they make only Lunar Orbs, then they could make 250 / 10.0 = 25.0 Lunar Orbs per week. This is represented by the point 0, 25.
- A Solar Disc takes 12.5 person-hours to make, so if they make only Solar Discs, then they could make 250 / 12.5 = 20.0 Solar Discs per week. This is represented by the point 20, 0.
- The line between those points represents all combinations of Lunar Orb and Solar Disc production that uses 250 person-hours per week.
- A production mix that uses less than the available 250 person-hours per week is below and to the left of the red line. For example, 5 of each product would use 10.0 person-hours per Lunar Orb * 5 Lunar Orbs per week + 12.5 person-hours per Solar Disc * 5 Solar Discs per week = 112.5 person-hours/week.
The current production of 14.0 Solar Discs and 7.5 Lunar Orbs per week is also shown on the chart. As intended, this production mix uses all the available 250 person-hours per week. However, we can see that there are many other (actually infinite) production mix solutions that use less than or equal to the team's available hours per week.
The feasible region
We have two more constraints, as shown in Figure 2:
- Materials. You have 500kg of materials available each week, represented by the blue line. A production mix that uses less than the available material is below and to the left of the blue line.
- Sales. You can sell up to twice as many Lunar Orbs as Solar Discs, represented by the purple line. A production mix that involves less than twice as many Lunar Orbs is below and to the right of the purple line.
In addition, we have implicit constraints that production volumes must be >=0, as only non-negative production make sense in this situation.
The combination of the explicit and implicit constraints defines the "feasible region", which is shaded in the chart. That is, the feasible region is the range of production mix volumes that comply with all the constraints simultaneously. For example, the current production of 14.0 Solar Discs and 7.5 Lunar Orbs is non-negative, equal to the People constraint, below and to the left of the Materials constraint, and below and to the right of the Sales constraint. Therefore, the current production mix is feasible.
Objective function contours
Your objective is to maximize gross profit. Each Lunar Orb makes a gross profit of $200 and each Solar Disc makes a gross profit of $80. Therefore, increasing production increases gross profit, though at different rates for the two products. We can represent the gross profit on the chart as a series of straight-line contours, like how we represent the constraints, with each contour representing a specific profit level.
Some gross profit contours, ranging from $1,000 to $6,000 per week, are shown in Figure 3.
For example, if you made only Solar Discs, then 25 Solar Discs would provide gross profit of 25 * $80 each = $2,000, represented by the point 25, 0. Similarly, 10 Lunar Orbs would provide gross profit of 10 * $200 each = $2,000, represented by the point 0, 10. The contour line between those two points represents all combinations of production mix that provide gross profit of $2,000.
Optimal linear solution
Looking at Figure 3, we can see where the current production mix's gross profit of $2,620 sits between the $2,000 and $3,000 contours. It is also apparent that the current production mix is not the point in the feasible region that results in the maximum gross profit.
Instead, Figure 4 shows that the optimal gross profit occurs where the Materials and Sales constraints intersect. That point corresponds to a production mix of 6.41 Solar Discs and 12.82 Lunar Orbs, resulting in a gross profit of just over $3,000 per week ($3,076.92 per week, to be exact).
It is important to note that this optimal solution occurs at the intersection of constraints – known as a "corner point", as it is a corner of the feasible region. In a linear program, an optimal solution always occurs at either a corner point or on a boundary of the feasible region between corner points (if the objective function coincides with that boundary, leading to a range of alternative optima).
Optimal integer solution
We can interpret the production mix of 6.41 Solar Discs and 12.82 Lunar Orbs as representing the average number of products to make each week. But we can only sell whole products, and we don't want to keep inventory from week to week, so what would happen if we require the production to be integers?
Figure 5 shows part of the feasible region, focused on the integer solutions (orange dots) near the optimal linear solution. Specifically:
- If we round the optimal linear solution of 6.41 Solar Discs and 12.82 Lunar Orbs to integers, then we have 6 Solar Discs and 13 Lunar Orbs. But that solution is outside the feasible region, so it is infeasible. It often happens that a rounded linear solution is not an optimal integer solution.
- The solution of 6 Solar Discs and 12 Lunar Orbs is feasible, but it has a relatively low objective function value.
- The solution of 8 Solar Discs and 12 Lunar Orbs has a better objective function value, but it is infeasible.
- In between, we have the solution of 7 Solar Discs and 12 Lunar Orbs, with an objective function value of $2,960. It is the best feasible integer solution, so it is the optimal integer solution.
It is always true that the optimal integer solution is either on the boundary of the feasible region (not necessarily at a corner point) or, as in this example, in the interior of the feasible region. In either case, the optimal integer solution can be no better than the optimal linear solution (though they may be equal).
In this example, the optimal integer solution has an objective function value that is 3.8% lower than the optimal linear solution.
Relax a constraint to find a better optimal solution
Returning to the linear model shown in Figure 4, the optimal solution occurs at the corner point where the Materials and Sales constraints intersect. That is, those constraints are both "binding", meaning that the solution uses all the 500kg of available materials and the number of Lunar Orbs equals two times the number of Solar Discs. Conversely, the People constraint is "slack" (not binding), meaning that the solution doesn't use all the available person-hours.
Given your current production mix, you are planning to reduce the standing order for materials, because you're currently not using all 500kg per week. However, the optimal linear solution does use all 500kg, so it isn't necessary to reduce the order. In addition, the current production mix was designed to use all the available person-hours, but the optimal solution doesn't use all the hours, which is not ideal.
Since you want to keep the team busy, you could increase the quantity of available materials until the optimal solution uses all 250 person-hours. This situation is shown in Figure 6, where the Materials constraint has been increased ("relaxed") to 600kg and the revised optimal solution is 7.69 Solar Discs and 15.38 Lunar Orbs, with a total gross profit of $3,692.31 per week. This solution occurs at the corner point where all three constraints intersect, though that isn't generally the case.
This revised optimal linear solution is a substantial improvement over your current solution. We've shifted the production mix in favor of Lunar Orbs, which makes sense given that they have a higher gross profit while consuming less time to make and needing only a moderate amount of additional materials. The result is a 41% increase in gross profit from $2,620.00 to $3,692.31 per week.
So far we've explored the situation graphically, by looking at the solution space. Next, we'll formulae the model in Excel and use Solver or OpenSolver to find the optimal solution.
Solver model
Objective function
We can implement our model design in Solver, as shown in Figure 7. Our objective is to maximize fTotalMargin.
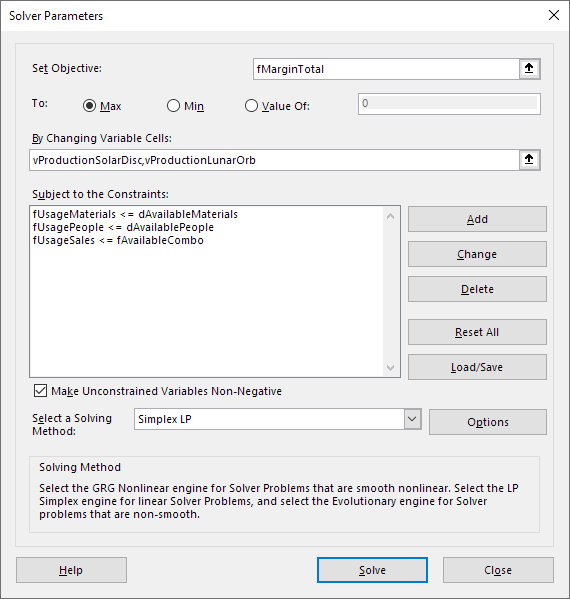
Variables
The model has just two variables:
vProductionSolarDisc. The number of Solar Discs to make per week.vProductionLunarOrb. The number of Lunar Orbs to make per week.
Constraints
The constraints are:
fUsageMaterials <= dAvailableMaterials. The Materials used must be less than or equal to the available quantity.fUsagePeople <= dAvailablePeople. The person-hours must be less than or equal to the available person-hours.fUsageSales <= fAvailableCombo. The combination of product sales must be within some ratio, e.g. sales of Lunar Orbs must be less than or equal to twice the sales of Solar Discs.
Solution method
This is a Linear Program (LP), so it can be solved efficiently using the Simplex method.
The model is small, so it can be solved quickly by either Solver or OpenSolver.
We can make the model a Mixed Integer Program (MIP), as we did in Figure 5, by adding constraints that require the production variables to be integers.
Analysis
Replicate the graphical analysis using Solver
We suggest that you use Solver or OpenSolver to replicate each step of the graphical analysis. Doing so will help you understand how the model works and how it behaves when given different data or constraints.
Conclusion
This model is an example of solving an optimal production mix problem in Excel.
Using an optimization model to explore the problem's solution space can help us to decide on a better production mix within current constraints and where to relax those constraints to find an even better solution.
If you would like to know more about this model, or you want help with your own models, then please contact us.
