Warehouse optimization: Model design

21 July 2023

In this article series we explore optimization of a "picking warehouse" – that is, a warehouse where we pick items off the shelves to fulfil a customer order. As a result, we improve the efficiency of our warehouse by a factor of three.

Specifically, we model the efficiency of:

• A variety of shelving layout designs.
• Positioning items on shelves according to order probability.
• Combining orders to achieve economies of scale.

Along the way, we assess many alternative warehouse designs, which requires solving more than a million shortest path problems (using Dijkstra's algorithm via the networkx library) and almost a million Travelling Salesman Problems (using the constraint solver in OR-Tools).

Unlike most of our blog articles, our focus isn't on the details of the model code – though the code and data are available to download. Instead, we focus on describing the steps we took to model the situation.

This first article describes and tests the main modelling setup. The subsequent articles will address our modelling questions.

Download the model

The model and data files are available on GitHub.

Situation

We operate an online retail shop. We ship items directly from our warehouse to customers.

When we receive a customer order, a "picker" collects the order details from the Begin point at the northern end of the warehouse. The picker walks around the warehouse picking the ordered items from the shelves. The picker then delivers the items to the End point for packaging and dispatch to the customer. The End point is adjacent to the Begin point. After completing an order, the picker returns to the Begin point, to collect the next order.

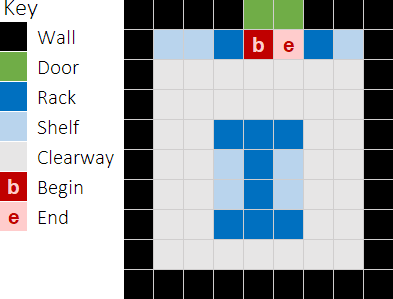
Despite a lot of innovation in warehouse design in recent years, most warehouses have a traditional layout consisting of long rows of shelves with the Begin/End points at one end. Our warehouse follows this design, which is shown in plan view in Figure 1.

As a modelling simplification, we have divided the warehouse into 1 metre square cells, each of which is colour-coded as followed:

• Black. External walls of the warehouse.
• Green. Doors to the external dock, where couriers collect the packages for delivery to customers.
• Red b. The Begin point, where pickers collect customer order details.
• Red e. The End point, where pickers drop off items for packaging and dispatch.
• Dark blue. Racks that contain shelves.
• Light blue. Shelves where items are stored. There is one type of item per shelf.
• Grey. Clearway between racks and the walls.

Our warehouse has 248 shelves arranged in four double-sided racks. The Begin/End points are against the North wall, next to the doors. To enable safe manoeuvring, we require a clearway of at least 2 metres between racks, between racks and walls, and between racks and the Begin/End points.

Questions

The current warehouse design works fine. However, our building lease expires soon, so we have an opportunity to relocate to a different building, which we'll either lease or build.

Observation of the current warehouse operations has identified significant cost due to the pickers spending a lot of time walking around the warehouse. For example, a round-trip from the Begin point to the furthest corner of the warehouse is about 90m, which takes about a minute. Additionally, we have noticed that some of our items are more popular than others. Currently items are positioned on shelves according to product category, without considering their popularity. Lastly, each order is picked individually, ensuring streamlined packaging and dispatch processes while minimizing the risk of order mix-ups. However, our pickers frequently express frustration about the substantial time spent returning to an area they have recently traversed for a previous order.

These observations lead us to ask if the efficiency of the picking process could be improved. Therefore, we want to answer three questions:

• Would a different rack/shelf layout design improve efficiency?
• What is the effect of positioning items according to order probability?
• Is there benefit in combining orders?

Model design

Represent the warehouse as a grid

A key aspect of our model design is representing the warehouse as a grid. This choice simplifies the modelling process by reducing the problem to a finite number of discrete points, rather than an infinite number of continuous points. While discretizing variables can make models more challenging to solve, in this situation it significantly streamlines the process. In the following sections, we will explore the reasons behind this design decision and the resulting benefits it brings to our overall approach.

Initially work with a small, test data set

Our warehouse has 250 points of interest – the Begin/End points and 248 shelves. Rather than dealing with the complexity of the full-scale situation, we'll initially work with a small, test version. This approach has several advantages, including:

• Simplicity. The full data set is quite complex, while a small data set is simple. This allows us to see all the data and analysis steps, without being overwhelmed by detail.
• Manual solution. With a simple model, we can manually verify that everything is working as expected or identify where it is not.
• Runtime. A small data set will solve much faster than a large one. This enables us to quickly iterate through the model design and build process, without waiting a long time for the model to run.

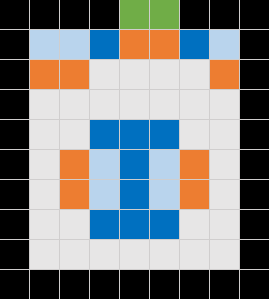
For developing the model we used the test warehouse layout shown in Figure 2. This layout has only seven shelves – located in one set of racks plus some shelves against the North wall.

A potential disadvantage of a small test data set is that it may not contain sufficient diversity to exhibit the full range of behaviours that exist in the full situation. One way to address this issue is to have multiple small data sets that have different characteristics. When building and testing the model, we used several test layouts.

Points of interest: Spots

When a picker is fulfilling a customer order, they start on the Begin cell, visit each shelf that contains an ordered item, then drop off the items on the End point cell.

When visiting a shelf, the picker doesn't go to the cell occupied by the shelf itself, as that is not physically possible. Instead, they go to a cell next to the shelf – that cell is called a "spot". Each spot is adjacent to a shelf, in a cardinal direction. So that the model can automatically identify a shelf's spot, given the layout, each shelf is assumed to have exactly one spot. This means that a shelf must be enclosed by walls, racks, or other shelves in all-but-one cardinal direction.

Figure 3 shows the spots, highlighted in orange, for our test layout. Two spots coincide with the Begin and End points. The other spots are adjacent to the shelves.

Our test warehouse layout is a grid of 10 rows by 9 columns, for a total of 90 cells. Since there are only seven shelves, with nine spots, this test layout is small enough for us to work with manually.

Note that our test layout doesn't allow two metres between the rack and the South wall, as required in the situation description. This doesn't matter for the purposes of testing, but it will be important for the full warehouse layout designs that we'll look at later.

Label all cells for easy reference

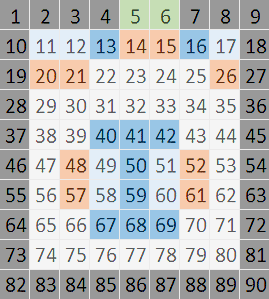
We need to start formalizing how we refer to the warehouse layout, so that our model can identify each cell. The first step is to give each cell a unique label, as shown in Figure 4.

That is, we label all cells starting with 1 for the Northwest cell, proceeding across each row towards the East, then finishing with 90 for the Southeast corner.

Using this labelling system, the Begin cell is 14 and the End cell is 15. The seven shelves are located at cells 11, 12, 17, 49, 51, 58, and 60. The nine spots are located at cells 14, 15, 20, 21, 26, 48, 52, 57, and 61 (noting that the Begin and End cells coincide with their spots).

The path that pickers take to pick items from shelves can be described as a Travelling Salesman Problem (TSP). We will use the labels to represent the TSP path.

Creating an adjacency graph

Before we can solve a TSP, we need to create a matrix of distances between each spot and every other spot.

In other situations, we might calculate the distance between spots using a variety of methods, including:

• Euclidean distance. The straight-line distance between spots.
• Manhattan method. The distance allowing for moves only in cardinal directions (like the grid structure of Manhattan city streets).
• Road distance. Actual distance, allowing for curves, etc. in the road.
• Cost function. Rather than physical distance, we might want to minimize some other function, like time or dollar cost.

In our situation, we need to account for arbitrary obstacles (racks and shelves), which substantially complicates navigation around the environment.

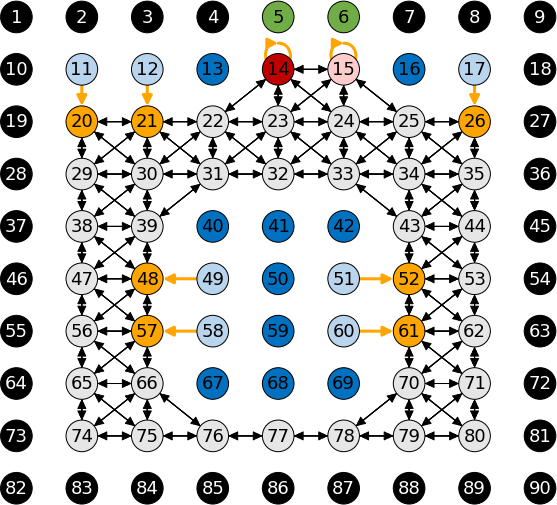
Our solution is to allow cardinal and diagonal steps from cell to cell, only when such a step is feasible. That is, we create an adjacency graph that describes, for every cell, which cells are directly reachable from that cell. Connections between cells are indicated by an arrow, as shown in Figure 5.

For example:

• Cell 11. This is a shelf. It is not reachable from any cell, because we don't go to a shelf cell, instead we go to its spot (as indicated by the orange arrow).
• Cell 20. This is the spot for the shelf in cell 11. We can get to cell 20 from cells 21, 29, and 30 because those cells are adjacent in a cardinal or diagonal direction. Likewise, we can get to cells 21, 29, and 30 from cell 20.
• Cell 16. This is a rack. The rack, door, and wall cells do not have any adjacency relationships because we do not visit any of those cells when picking items. In fact, we need to explicitly avoid visiting those types of cells, as they are obstacles.
• Cell 70. This is a clearway cell, which we may visit on the way to a spot. It is adjacent to cells 61, 62, 71, 78, 79, and 80.

There are special cases for the Begin and End cells. When solving to find an optimal TSP path, OR-Tools requires a closed path – that is, a path that starts and ends at the same point. We want to start and end at different points, so we create a dummy node that is zero distance from the Begin and End cells. In the diagram, this is represented as an arrow to the same cell.

The adjacency graph is created automatically by the model, given the layout data.

Shortest path between spots

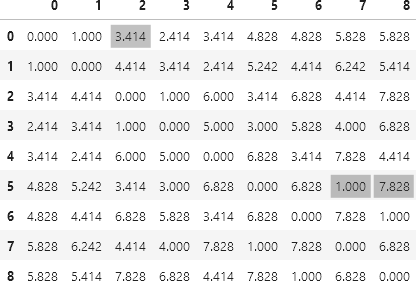
Given the adjacency graph, we can determine the shortest path between every pair of spots. Since our grid is defined to be 1m x 1m squares, the distance between cells in cardinal directions is 1m and in diagonal directions is 1.414m (= square root of 2m).

The result for our test layout is shown in Figure 6. The matrix is symmetrical, meaning that, for example, the distance of 4.414m from Spot 2 to Spot 7 is the same as the distance from Spot 7 to Spot 2.

The distance matrix always has the Begin and End cells in positions 0 and 1 respectively. The remaining positions correspond to the spots in ascending numerical order. For example, as highlighted in the figure:

• The shortest distance between the Begin cell (position 0) and the spot at cell 20 (position 2) is 3.414. That is, one diagonal step and two cardinal steps.
• The shortest distance between the spot at cell 48 (position 5) and the spot at cell 57 (position 7) is 1.000. That is, one cardinal step.
• The shortest distance between the spot at cell 48 (position 5) and the spot at cell 61 (position 8) is 7.828. That is, two diagonal steps and five cardinal steps. There are alternative solutions that go around the rack either to the North or the South. We're indifferent about alternative solutions of the same length.

We use the networkx library to populate the shortest path matrix. When developing the model, we initially used OR-Tools to find the shortest paths, since we planned to use OR-Tools to solve the Travelling Salesman Problems. While OR-Tools worked fine, it is much slower than networkx for this task – by more than an order of magnitude. Therefore, we changed the model to use networkx instead.

Note that both networkx and OR-Tools occasionally return a path that is slightly longer than optimal. Such sub-optimal solutions are uncommon and the difference from the optimal length is small, so the effect is not material.

Fulfil a customer order: Tour

All of our questions relate to the efficiency of different warehouse designs. We can express the efficiency in terms of the average distance needed to fulfil customer orders. We can determine the shortest path required to fulfil a specific customer order by representing the situation as a Travelling Salesman Problem (TSP).

We use OR-Tools to find the optimal TSP tour for a given customer order. We also tried using networkx to solve the TSP tours. Although networkx is many times faster than OR-Tools, it occasionally returns a path than is much longer than optimal, which materially effects the average. OR-Tools also occasional returns a sub-optimal length, though the error is much smaller.

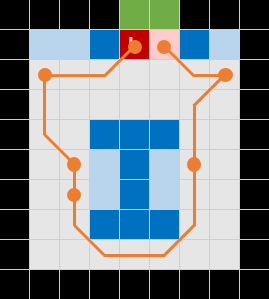
Figure 7 shows how a picker could fulfil an example customer order. The customer has ordered five items. The picker starts on the Begin cell, then moves in an anti-clockwise path around the warehouse, stopping at the spots adjacent to the shelves where the ordered items are located. The picker then finishes at the End cell. For other orders, the shortest path might be clockwise, or even just there and back.

The path that the picker takes is called a tour. The example tour can be represented as: 14 → 20 → 48 → 57 → 52 → 26 → 15 (using the cell labels defined in Figure 4). The length of our example tour is 21.484m, consisting of 13 moves from cell to cell in a cardinal direction (each of length 1m), plus 6 moves in a diagonal direction (each of length 1.414m). There are multiple alternative optimal paths with this length.

Note that allowing the picker to move only in cardinal directions or diagonally is a modelling approximation that we've chosen to make. In practice, a picker could achieve a slightly shorter tour by walking in straight lines in any direction. However, given that the picker must walk around the racks (and potentially other obstacles), it is much easier to model steps to an adjacent cell only in cardinal and diagonal directions. Otherwise, we would need to find some way to model the distance between spots in any direction while allowing for arbitrary obstacles – a complex problem.

The inaccuracy introduced by this approximation is small and unlikely to be material. This approximation is in addition to the approximation of representing the warehouse as a grid of 1m x 1m cells. It is important to recognize that modelling almost always involves making approximations, usually as a trade-off to reduce model complexity and/or reduce runtime.

Picking efficiency over all orders

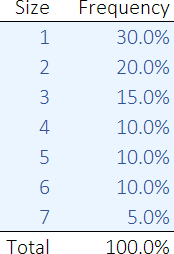
We have seven items in our test warehouse layout. Our customers can purchase between one and seven items in an order. As shown in Figure 8, the most common order size is one item, at 30% of all orders, while only 5% of customers purchase all seven items in an order. Consequently, the most common tour will be to pick just one item – consisting of a tour visiting only three spots: Begin, the item's spot, and End.

For assessing the efficiency of a warehouse layout, we want to determine the average tour length across all customer orders. For our test layout, there are only 127 possible combinations of seven items. This is small enough that we could find the optimal tour for each of them.

However, our actual warehouse has 248 items, with customers ordering up to 10 items per order. This leads to an enormous number of possible combinations (around 2x10¹⁷) – far more than we could ever compute.

Therefore, we'll adopt a simulation approach of generating random orders, with an order size that follows the frequency shown in Figure 8. We will then repeat the modelling a specified number of times, to obtain a sample size that provides a reasonable estimate of the average tour length.

Initially we'll assume that all items are equally likely to be ordered. This is equivalent to assuming that items are located on random shelves, with positions that are unrelated to their order probability. Later we'll examine positioning of items according to their order probability.

Putting it all together

When we put together all the elements described above, we can determine the average length of tours required to pick customer orders. To do that we built a model in Python, using the networkx and OR-Tools libraries.

Each warehouse design consists of two Excel files, one for the layout and one to specify the order size frequency. In addition, there are several options that we need to specify, each of which is a global value in the Python code.

For the test layout, we use the following global values:

• Warehouse layout, as shown in Figure 2: DesignFile = 'Layout-small.xlsx'
• Order size frequency, as shown in Figure 8: FreqFile = 'Frequency-small.xlsx'
• Minimum number of items per order: MinOrderItems = 1
• Maximum number of items per order: MaxOrderItems = 7
• Sample size: NumIters = 1000
• Ratio of most frequently ordered item to least frequently ordered item: ItemRatio = 1

Note that the file Layout-small.xlsx contains instructions for creating additional warehouse designs.

Results for test warehouse layout

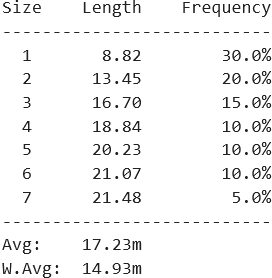
Figure 9 shows the results for our test layout. With a sample size of 1,000 simulated orders, the runtime is about 3 minutes.

The model calculates the average length of tours to pick orders of size one to seven items. We then calculate the overall average tour length:

• Simple average. Ignoring the frequency of order sizes, the simple average tour length is 17.23m.
• Weighted average. Allowing for the frequency of order sizes, the weighted average tour length is 14.93m. The weighted average is less than the simple average because although orders with more items will usually have longer tours, they are much less common.

As a check, we can directly calculate the expected length of orders for one item. That is, since each item is equally likely to be ordered, the expected length is the average of tours from Begin to a shelf's spot to End, for all items. That average is 8.87m, so our sample average of 8.82m is very close, suggesting that a sample size of 1,000 orders is sufficient.

In addition, this result suggests that there is an economies of scale effect. That is, the average distance per item is 8.82m for an order of one item (= 8.82 / 1), compared with 3.07m (= 21.48 / 7) for an order of seven items. We'll further explore this effect later.

Comparison with a different layout

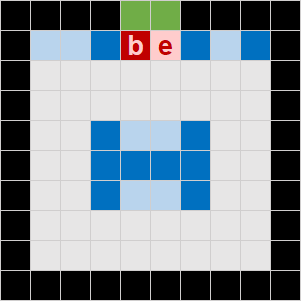
To determine the relative efficiency of warehouse layouts, we can devise different layouts and re-run the model. We then compare the average tour lengths to determine which design is more efficient.

For example, an alternative test layout is shown in Figure 10. We've rotated the central rack by 90 degrees, to see if that improves efficiency. We've also made the warehouse 1m wider, to provide the required 2m clearway all the way around the rack – though the shortest paths will never use those extra cells, so they make no difference to the average tour lengths.

To ensure a fair comparison between layouts, it is important that the designs have the same number of shelves. There may be different numbers of other cells – for example, this design has one more rack cell, two more wall cells, and seven more clearway cells.

The weighted average tour length for this alternative design is 15.22m. That's 1.9% longer than the 14.93m of the previous test design. Therefore, this design is not quite as efficient as the previous one.

Conclusion

In this article we've described a model for assessing warehouse layout designs. Our objective is to compare the relative efficiency of the designs, in terms of the average distance required to pick a representative sample of orders.

The model is built in Python. It uses the networkx and OR-Tools libraries to solve shortest path and Travelling Salesman Problem components of the overall model. All model files are available on GitHub.

In the next article we apply the model to a variety of full-size warehouse designs, to compare their relative efficiencies.

If you would like to know more about this model, or you want help with your own models, then please contact us.