Warehouse optimization: Assessing layouts

7 August 2023

This is the second article in our series looking at improving the efficiency of a picking warehouse.

In the previous article, we described our Python model for calculating the efficiency of the warehouse layout. Efficiency is defined in terms of the average distance that the pickers travel to fulfil customer orders.

In this article, we'll apply that model to assessing alternative warehouse layout designs, seeking to improve efficiency relative to our current warehouse's design. We present only a selection of the many designs that we assessed.

Our focus isn't on the details of the model code – though the code and data are available to download for you to learn from and experiment with. Instead, we'll focus on describing application of the model to answering our three modelling questions:

• Would a different rack/shelf layout design improve efficiency?
• What is the effect of positioning items according to order probability?
• Is there benefit in combining orders?

This article answers the first question. The next article will answer the other two questions.

Challenge: Design a better layout, while meeting the design criteria.
Show us your better design

Download the model

The model and data files are available on GitHub.

Situation

We operate an online retail shop. We ship items directly from our warehouse to customers.

When we receive a customer order, a "picker" collects the order details from the Begin point at the northern end of the warehouse. The picker walks around the warehouse picking the ordered items from the shelves. The picker then delivers the items to the End point for packaging and dispatch to the customer. The End point is adjacent to the Begin point. After completing an order, the picker returns to the Begin point, to collect the next order.

The order size varies between one item (30% of orders) and ten items (1% of orders) per order, as defined in the Frequency-full.xlsx data file.

Layouts

Layout A: Current warehouse

Despite a lot of innovation in warehouse design in recent years, most warehouses have a traditional layout consisting of long rows of shelves with the Begin/End points at one end. Our current warehouse follows this design, as shown in Figure 1. As described in the previous article, we've divided the warehouse into 1m x 1m squares, which are colour-coded according to the Key in the figure.

Our current warehouse has 248 shelves arranged in four double-sided racks. The Begin/End points are against the North wall, next to the doors. To enable safe manoeuvring, we require a clearway of at least 2 metres between racks, between racks and walls, and between racks and the Begin/End points.

To assess the efficiency of the current layout, we use the following global values in the model:

• Warehouse layout: DesignFile = 'Layout-A.xlsx'
• Order size frequency: FreqFile = 'Frequency-full.xlsx'
• Minimum number of items per order: MinOrderItems = 1
• Maximum number of items per order: MaxOrderItems = 10
• Sample size: NumIters = 1000
• Ratio of most frequently ordered item to least frequently ordered item: ItemRatio = 1

After running the model, the results for Layout A are:

• Weighted-average tour length: 86.07m.
• Weighted-average tour length per item: 31.27m.
• Warehouse area: 960m².
• Utilization: 29.7% (shelf cells / total interior cells excluding walls and doors).
• Squareness: 1.67 (ratio of longest side's length to shortest side's length).

These results are the benchmarks against which other layout designs are assessed.

With a sample size of 1,000 iterations, the model takes about two hours to run. Generating the matrix of distances from every spot and every other spot is relatively quick, taking less than one minute to solve 31,125 (= [250^2 - 250] / 2) shortest path problems using networkx. Almost all the time is spent solving the Travelling Salesman Problems (TSP) using OR-Tools, of which there are 10,000 (= 10 order lengths x 1,000 iterations) tours per layout.

Layout B: Closer to square

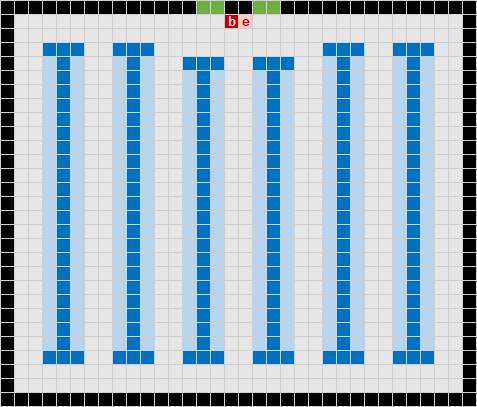
Figure 2 shows our first alternative design, Layout B. We think a more compact design might be more efficient. So, we rearrange the racks in a warehouse that is almost square, with six racks instead of four.

Importantly, to ensure a fair comparison, this design – like all our alternative designs – also has 248 shelves. Note that the two central racks are shorter than the others, to provide the required 2m clearway between the Begin/End points and the racks.

The results for Layout B (with change relative to Layout A) are:

• Weighted-average tour length: 78.15m (-9.2%).
• Weighted-average tour length per item: 27.56m (-11.9%).
• Warehouse area: 986m² (+2.7%).
• Utilization: 28.7% (-1.0%).
• Squareness: 1.17 (-0.50).

Although this design is substantially squarer, it has a slightly larger area. This somewhat counter-intuitive effect occurs because a squarer design requires more racks and clearway cells, as indicated by a lower utilization.

Nonetheless, this layout is a significant 9.2% improvement in efficiency compared with Layout A, indicating that this squarer warehouse design is better.

Layout C and Layout D: Central aisle

An issue with both Layout A and Layout B is that the racks are quite long. To access a shelf that isn't in the current aisle, the picker must go around the end of the racks – which can be a long way.

To address this issue, we introduce an aisle in the centre of the racks. Layout C orients the racks West-East with a North-South aisle, while Layout D orients the racks North-South with a West-East aisle, as shown in Figure 3.

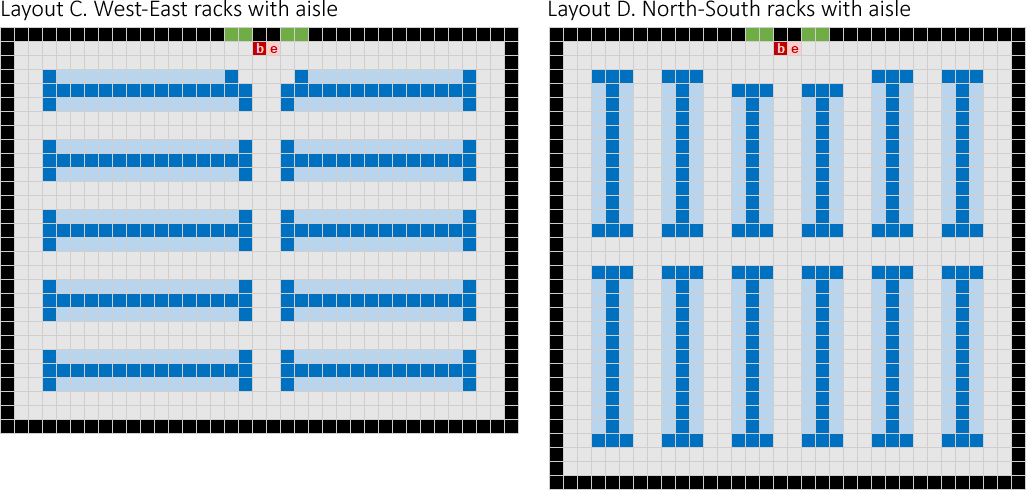
The results for Layout C are:

• Weighted-average tour length: 73.68m (-14.4%).
• Weighted-average tour length per item: 27.03m (-13.6%).
• Warehouse area: 1,073m² (+11.8%).
• Utilization: 26.2% (-3.5%).
• Squareness: 1.28 (-0.39).

The results for Layout D are:

• Weighted-average tour length: 72.60m (-15.7%).
• Weighted-average tour length per item: 26.77m (-14.4%).
• Warehouse area: 1,122m² (+16.9%).
• Utilization: 25.0% (-4.7%).
• Squareness: 1.03 (-0.64).

The aisle improves efficiency, though it also makes the warehouses larger, so there is a trade-off. The utilization is lower for both layouts, due to the addition of the aisle cells.

We speculate that Layout D is slightly more efficient than Layout C because the racks are oriented towards the Begin/End points, which provides easier access, and because it is nearly square.

Layout E and Layout F: Shelves around walls

Another way to make the warehouse more compact is to put some shelves around the perimeter, against the walls. Layouts E and F do this, as shown in Figure 4.

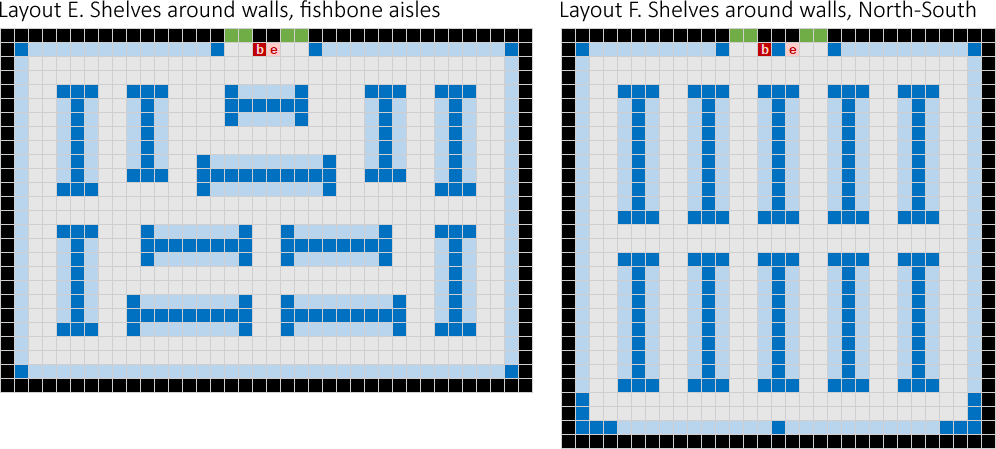
Layout E also adopts a "fishbone" design. That is, some racks are oriented West-East while others are North-South, with diagonal aisles that meet at the Begin/End points. The idea of having diagonal aisles is to provide more direct, straight-line access to the far corners of the warehouse and the racks along the way.

The results for Layout E are:

• Weighted-average tour length: 68.63m (-20.3%).
• Weighted-average tour length per item: 25.95m (-17.0%).
• Warehouse area: 988m² (+2.9%).
• Utilization: 28.7% (-1.0%).
• Squareness: 1.46 (-0.21).

Layout F is like Layout D, except that we need only five racks, as some shelves are against the walls.

The results for Layout F are:

• Weighted-average tour length: 65.34m (-24.1%).
• Weighted-average tour length per item: 24.70m (-21.0%).
• Warehouse area: 930m² (-3.1%).
• Utilization: 30.5% (+0.8%).
• Squareness: 1.03 (-0.64).

In some contexts, the fishbone layout can be a very efficient design – we speculate that it doesn't perform as well as it could because our warehouse is relatively small and the model uses a grid approximation, which makes the racks relatively large compared with the shelves.

Layout F is very similar to Layout D, though placing some shelves against the walls makes the warehouse significantly smaller and more efficient.

Layout G and Layout H: Begin/End in the centre

Layout F is a substantial improvement compared with Layout A. But having the Begin/End points on the North wall positions them a long way from some of the shelves.

Positioning the Begin/End points at the centre of the warehouse should further reduce the average distance to the shelves. So, we do that in Layout G, as shown in Figure 5. We also orient the shelves in a West-East direction, to make the aisles accessible from the warehouse's centre.

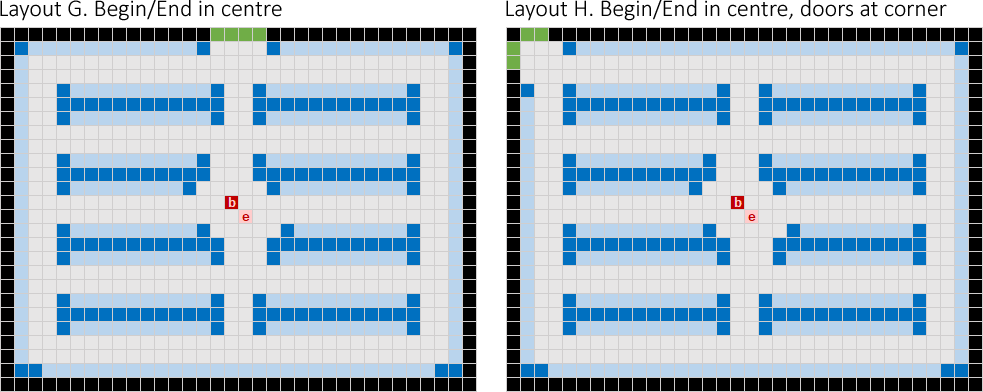
Since the Begin/End points are no longer adjacent to the doors, we'll need some method for transporting the orders to the external dock for collection by the couriers. One solution is to install a conveyor from the End point to the doors. We could position the conveyor overhead, so it doesn't interfere with easy movement around the warehouse.

The results for Layout G are:

• Weighted-average tour length: 58.36m (-32.2%).
• Weighted-average tour length per item: 20.19m (-35.4%).
• Warehouse area: 884m² (-7.9%).
• Utilization: 32.3% (+2.6%).
• Squareness: 1.31 (-0.36).

The result for Layout G is substantial improvement even compared with Layout F. But perhaps we can do better by moving the doors to a corner, as we do in Layout H. The idea is that the corners are further away from the centre compared with the middle of the North wall, so placing shelves against the relatively close mid-wall position is more efficient.

The results for Layout H are:

• Weighted-average tour length: 57.38m (-33.3%).
• Weighted-average tour length per item: 19.71m (-37.0%).
• Warehouse area: 884m² (-7.9%).
• Utilization: 32.3% (+2.6%).
• Squareness: 1.31 (-0.36).

Layout H is a small improvement relative to Layout G. Even though Layout G and Layout H are less square than Layout F, the tours are significantly shorter, indicating the benefit of placing the Begin/End points in the centre of the warehouse.

Layout I: Squarer version of Layout H

While Layout H is our most efficient so far, it isn't as square as it could be. We noted earlier that squarer layouts tend to be more efficient. So, Layout I is an almost square version of Layout H, as shown in Figure 6.

The results for Layout I are:

• Weighted-average tour length: 57.52m (-33.2%).
• Weighted-average tour length per item: 19.81m (-36.6%).
• Warehouse area: 930m² (-3.1%).
• Utilization: 30.5% (+0.8%).
• Squareness: 1.03 (-0.64).

Making the layout squarer also increased the area relative to Layout H, though it is still smaller than Layout A. Even though Layout I is squarer, it is slightly less efficient than Layout H. This reflects the larger area and lower utilization of Layout I.

However, the difference in weighted-average tour length between Layout H and Layout I of 0.14m is not statistically significant. That is, to estimate the standard deviation of the weighted-average tour length, we ran Layout I multiple times. With a sample size of 1,000 orders, the standard deviation of the weighted-average tour lengths is about 0.15m, so Layouts H and I differ by about one standard deviation.

Summary statistics

Figure 7 shows some summary statistics for our selected layouts. Layout H is the most efficient design, with an average tour length per item that is 37.0% shorter than for Layout A. Layout I has essentially the same efficiency as Layout H, with an even more square design.

The improved efficiency of Layouts H and I, relative to our current warehouse Layout A, is primarily due to five design changes:

• A more compact design, closer to being square.
• Putting some shelves against the walls, making better use of the perimeter space.
• Having a central aisle, reducing the distance to adjacent racks.
• Placing the Begin/End points at the centre of the warehouse.
• Having the doors in a corner of the warehouse, rather than in the middle of a wall.

Both Layout H and Layout I have average tour lengths that are about 33% less than for Layout A. Similarly, their average tour length per item is about 37% more efficient than for Layout A.

Conclusion

In this article we've applied our warehouse layout model, as described in the previous article, to assess a variety of warehouse designs. Our best designs reduce the picker's average tour length by a third, which is a substantial improvement relative to our current warehouse.

The model is built in Python. It uses the networkx and OR-Tools libraries to solve shortest path and Travelling Salesman Problem components of the overall model. All model files are available on GitHub.

In the next article we will apply the model to answering our two other questions about positioning items according to order probability and combining orders.

If you would like to know more about this model, or you want help with your own models, then please contact us.