23 August 2023

This is the third, and final, article in our series looking at improving the efficiency of a picking warehouse.
In the previous article, we assessed a variety of layout designs for our warehouse. That analysis answered our first modelling question, "Would a different rack/shelf layout design improve efficiency?", by identifying a layout that is 33% more efficient than the current design.
In this article, we extend the analysis to answer our other two modelling questions. That is, can the efficiency of the picking process be further improved by:
- Positioning items according to order probability?
- Combining orders?
Download the model
The model and data files are available on GitHub.
The warehouse designs are defined in data files like Layout-A.xlsx, Layout-B.xlsx, etc. Instructions for creating your own layouts, including the design criteria, are in the Layout-small.xlsx file.
Situation
We operate an online retail shop, and we ship items directly from our warehouse to customers.
When we receive a customer order, a "picker" collects the order details from the Begin point. The picker walks around the warehouse picking the ordered items from the shelves. The picker then delivers the items to the End point for packaging and dispatch to the customer. The End point is adjacent to the Begin point. After completing an order, the picker returns to the Begin point, to collect the next order.
The order size varies between one item (30% of orders) and ten items (1% of orders) per order, as defined in the Frequency-full.xlsx data file.
Positioning items according to order frequency
Order frequency distribution
In our previous analysis, we assumed that all items are equally likely to be ordered. Therefore, the positioning of items in the warehouse does not matter. This assumption allowed us to focus on the effect that the warehouse layout design has on the picking process efficiency.
But in practice, some items are much more popular than others. To explore the effect of order frequency on warehouse efficiency, we model the order popularity using a distribution that is defined in terms of a ratio parameter. That is, the ratio of the most popular to the least popular item. For example, returning to the small test warehouse layout, Figure 1 shows distributions of order frequency for the 7 items, given ratios of 1 and 20:
- Ratio = 1. All items are equally likely to be ordered. This is what we assumed in the previous articles
- Ratio = 20. The most popular item is 20 times more likely to be ordered than the least popular item.
In this article, we'll focus on an order frequency ratio of 20. The model allows this parameter to be changed, to see what effect that has on the picking efficiency.
Positioning of items in test layout
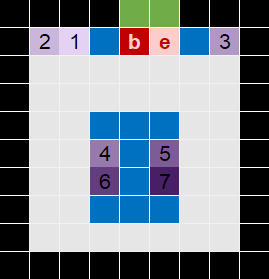
Given the order frequency, we want to position the items according to their popularity. That is, to minimize travel distance for the pickers, we want popular items to be close to the Begin and End points in the warehouse. Conversely, items that are seldom ordered should be positioned furthest from the Begin and End points.
We can represent the positioning on a warehouse layout design using lighter/darker shading. For example, given a ratio of 20, we position the test warehouse's 7 products as shown in Figure 2.
That is, the most popular item, #1, is positioned closest to the Begin point (b) – so that shelf has the lightest purple shade. Similarly, the second and third most popular items are positioned close to the Begin point, along the North wall. Continuing the pattern, the other products are positioned according to the shelves' distance from the Begin point – with the least popular item positioned on the shelf with the darkest shading.
Our test warehouse design is symmetrical. So, for example, the distance from b to 6 is the same as the distance from b to 7. Since we're indifferent between where we place items of the same distance, we position the higher probability items from West to East.
Positioning of items by probability in improved warehouse layout

We can apply the same process to the improved warehouse Layout H we found in the previous article.
Our improved layout has 248 shelves arranged as shown in Figure 3. The most frequently ordered items are positioned closest to the Begin point, which is at the centre of the warehouse. Items that are ordered less frequently are positioned further away – indicated by a darker shading of their shelves.
Note that the positioning is based on the optimal shortest path distance from the Begin point to each shelf. We considered a simpler approach of using the Euclidean distance from the Begin point to a shelf. However, that approach significantly distorted the positioning, especially for some warehouse layout designs. Therefore, this more complex design is better.
Impact of positioning by probability
To assess the efficiency impact of positioning items according to their order probability, we use the following global values in the model:
- Warehouse layout:
DesignFile = 'Layout-H.xlsx' - Order size frequency:
FreqFile = 'Frequency-full.xlsx' - Minimum number of items per order:
MinOrderItems = 1 - Maximum number of items per order:
MaxOrderItems = 10 - Sample size:
NumIters = 1000 - Ratio of most frequently ordered item to least frequently ordered item:
ItemRatio = 20
After running the model, the results for Layout H (and change from our current warehouse) are:
- Weighted-average tour length: 46.34m (-46.2%).
- Weighted-average tour length per item: 15.42m (-50.7%).
For our current warehouse, the average tour length per item is 31.27m. For the improved design, Layout H, the average tour length per item is 19.81m – a reduction of 36.6%. When we position items by probability in Layout H, the average tour length per item is 15.42m – which is 50.7% less than for the current layout.
Our second modelling question is: "Can the efficiency of the picking process be further improved by positioning items according to order probability?". The answer is a clear "yes". Using the improved layout and positioning items according to order probability halves the distance our pickers need to walk to pick each item. This is a substantial improvement.
Additional impact of combining orders
Our third modelling question relates to the potential for further efficiency from combining orders.
In Figure 9 of the first article in this series we identified an economies-of-scale effect as order size increases. We expect that it is possible to gain further efficiency improvements by combining orders, to take advantage of this economies-of-scale effect.
Figure 4 shows how we can simulate the effect of combining orders. That is, instead of picking each order separately, we combine orders according to simple rules:
- As orders arrive, we combine orders up to a maximum of 10 items.
- We do not split orders.
For example, we combine the first three orders, which together have 10 items. The next two orders have a combined 5 items, but the next order of 6 items would be too many, so we combine only orders 4 and 5. We pick orders 6 and 7 separately. Then we combine orders 8 and 9, and we also combine orders 10, 11, 12, and 13.
The effect of applying this procedure to Layout H (with items positioned according to probability), compared with our current warehouse, is that:
- The number of items per tour more than doubles, from 3.57 to 8.02 items/tour (because we combined orders).
- The average length of each tour decreases by 5%, from 86.07m to 81.35m (because of the item positioning and economies of scale).
- The average distance per item falls by two thirds, from 31.27m to 10.45m.
The effect of positioning items according to order probability reduced the average tour length per item by about 50%. Adding our procedure for combining orders further reduces the average tour length per item for a total reduction of about 67%.
Therefore, we can answer our third modelling question in the affirmative – there is significant benefit due to combining orders.
Summary of design improvements
Figure 5 shows a summary of our findings. That is:
- Our current warehouse design requires the pickers to travel an average distance of 31.27m per item picked.
- Layout H is the most efficient design, with an average tour length per item that is 36.6% shorter than the current warehouse.
- Positioning items according to order probability further improves efficiency, halving the average tour length per item compared with the current warehouse.
- Combining orders adds a further improvement, reducing the average tour length per item overall by two-thirds.
This modelling shows that it is possible to make major improvements in the efficiency of our warehouse. Each of the changes makes a significant impact, and the combined effect is substantial.
Conclusion
In this article we complete the modelling of our picking warehouse. The design improvements lead to substantial savings – cutting our picking cost by two-thirds.
The model is built in Python, using the networkx and OR-Tools libraries to solve shortest path and Travelling Salesman Problems. All the model files are available on GitHub, so you can explore how the model works.
If you would like to know more about this model, or you want help with your own models, then please contact us.
