13 May 2022
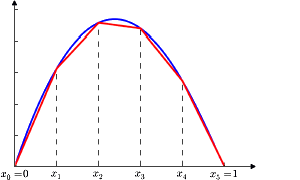
In the real world, we often encounter non-linear relationships in the systems we're modelling. But non-linearities can be difficult to model and even more difficult to solve to optimality.
The recently-published paper "Transformation and linearization techniques in optimization: A state-of-the-art survey" presents a detailed description of transformations and linearizations for a variety of non-linear relationships.
According to the paper's abstract:
To formulate a real-world optimization problem, it is sometimes necessary to adopt a set of non-linear terms in the mathematical formulation to capture specific operational characteristics of that decision problem. However, the use of non-linear terms generally increases computational complexity of the optimization model and the computational time required to solve it.
This motivates the scientific community to develop efficient transformation and linearization approaches for the optimization models that have non-linear terms. Such transformations and linearizations are expected to decrease the computational complexity of the original non-linear optimization models and, ultimately, facilitate decision making.
Asghari et al. (2022). "Transformation and linearization techniques in optimization: A state-of-the-art survey"
The transformation and linearization techniques described in the paper include:
- Multiplication of binary variables.
- Multiplication of binary and continuous variables.
- Multiplication of continuous variables.
- Maximum/minimum operators.
- Absolute value function.
- Floor and ceiling functions.
- Square root function.
- Multiple breakpoint function.
- Piecewise linear approximating functions.
- Log-linearization via Taylor series approximation.
- A new technique for linearizing square root terms by means of transformation.
The detailed descriptions in this paper make a good complement to the booklet MIP formulations and linearizations that we've mentioned previously.
Download the full paper: Transformation and linearization techniques in optimization: A state-of-the-art survey ![]()
If you need help transforming your non-linear model into a linear model, then please contact us.
