Solver Max - Green manufacturing via cutting patterns

20 August 2021

In this article we replicate a wood-cutting model from a published academic paper, "An application of cutting-stock problem in green manufacturing: A case study of wooden pallet industry". A key motivation of the case study is the minimization of waste, as a means of reducing the manufacturer's environmental impact.

The paper's model is built in Excel and solved using OpenSolver, so we do the same. More importantly, the paper illustrates a useful pattern selection technique for formulating and solving large one-dimensional cutting problems.

We focus on replicating the paper's model – though, surprisingly, we obtain a better result.

Download the models

The model is available on GitHub.

Situation

The situation is described in the paper's abstract:

The cutting-stock problem is used to minimize the impact of wasting material during the stock cutting process. The linear programming model is developed and implemented on Microsoft Excel to solve for the optimal cutting plan with the criteria of minimizing material waste.

The case study of pine wood stock cutting in wooden pallet industry demonstrates the benefit of using the approach in terms of reducing production cost and carbon emission.

The results show that waste can be reduced up to 70.86% resulting in a cost reduction of 977,352 Baht/year. The amount of carbon dioxide equivalent emitted from the life cycle of pine wood is reduced by 22,713 kg CO₂-e/year or approximately 5.32% reduction.
Wattanasiriseth, P. & Krairit, A. (2019). "An application of cutting-stock problem in green manufacturing: A case study of wooden pallet industry"

A link to the paper is available at the end of this article. We suggest that you read the paper, to understand the context and what the authors are looking to achieve.

Model design

A cutting patterns approach

In a previous blog article, Wire cutting, we designed and built a model for cutting wire to fulfil a customer's order for wire pieces of specified lengths. The model assigned each required piece to a stock item while minimizing waste. In this article, we solve a similar problem using a very different approach:

First, we enumerate all possible ways in which the required pieces can be cut from the available stock. That is, we create a list of "cutting patterns".
Then we select the combination of cutting patterns that fulfils the cutting requirements while minimizing the overall off-cut waste.

This approach of using pattern selection can be an efficient way to handle large cutting, packing, scheduling, and location problems.

Demand

Figure 1 shows the demand for cut wood pieces that we need to fulfil. That is, we need to cut a total of 8,899 pieces of 7 different sizes (labelled A to G). The shortest piece is 980 mm long, while the longest piece is 2,316 mm long, with total demand of over 11 linear kilometres of cut wood.

In our Wire cutting example, we needed to cut only 10 pieces. Here we need to cut almost nine thousand pieces. Our formulation for the wire cutting model could be scaled to handle a larger number of pieces, but it would not work well for a problem of this magnitude. That's where the cutting pattern approach becomes useful.

Stock items

Our stock items are very simple. The stock wood we're using is available in three lengths: 4,800 mm, 5,400 mm, and 6,000 mm. All 3 stock items have width of 150 mm and height of 100 mm, to match the width and height of the required cut pieces.

We assume that supply of the stock items is unlimited. We just need to work out how many of each size to order from our supplier.

What is a cutting pattern?

A cutting pattern is a design for cutting some required pieces from a stock item. For example, Figure 2 shows two cutting patterns given a stock item of length 4,800 mm and some of the pieces that we need to cut:

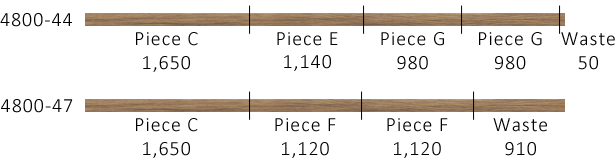
Pattern 4800-44. 1 x Piece C, 1 x Piece E, and 2 x Piece G. The pieces total 1,650 + 1,140 + 2 x 980 = 4,750 mm, leaving a waste off-cut of 50 mm.
Pattern 4800-47. 1 x Piece C, and 2 x Piece F. The pieces total 1,650 + 2 x 1,120 = 3,890 mm, leaving an off-cut of 910 mm. Our shortest required piece has a length of 980 mm, so the 910 mm off-cut is waste (it may be useful for a different customer order, but we ignore that possibility).

Note that the patterns are identified with the stock length and an index number that together provide a unique label for each pattern. Pattern 4800-44 is quite efficient, with only a small off-cut of 50 mm (1.04% of the stock item's length). Pattern 4800-47 has a much larger off-cut of 910 mm (18.96% of the stock item's length). An optimal solution is unlikely to use Pattern 4800-47, but we include it for completeness.

Following the convention in the paper, we ignore any length lost by making the cuts.

Enumerate all cutting patterns

So far we've designed two cutting patterns. How many others are possible?

That isn't a simple question to answer. To help us, we wrote a VBA procedure that generates all potential combinations of our 3 stock sizes and 7 required pieces. It turns out that there are over 80,000 potential combinations, most of which are infeasible. The procedure discards all combinations that are infeasible, which leaves a total of 526 cutting patterns that we need to consider: 109 patterns for the 4,800 mm stock, 164 patterns for the 5,400 mm stock, and 253 patterns for the 6,000 mm stock.

Note that our enumeration procedure differs from the enumeration procedure described in the paper. That's because we adapted some VBA that we already had, rather than trying to exactly replicate the paper's procedure. More detail of our enumeration procedure is available in the cuttingpatterns.xlsm file.

Select the optimal cutting patterns

Given a list of cutting patterns, the model is straightforward: Decide how many of each pattern to use, so that we cut the required number of pieces of each size, while meeting the objective of minimizing the total off-cut waste.

Model formulation

Our model formulation is shown in Figure 3.

That is:

Equation (1). We want to minimize the weighted sum of three components: Length of waste, Number of patterns used, and Number of cuts.
Equation (2). Ensure that the supply of cut pieces equals the demand for pieces.
Equation (3). Cuts are made from a pattern only if that pattern is being used.

Figure 3. Mathematical formulation

\begin{alignat*}{1} & \text{Objective} \\ & \quad \text{Min } fObjective \quad &= &\quad \text{dWeight}_{1} \times \sum_{p=1}^n (\text{dWaste}_{p} \times vCount_{p}) \\ &&& + \text{dWeight}_{2} \times \sum_{p=1}^n (vUsePattern_{p}) \\ &&& + \text{dWeight}_{3} \times \sum_{p=1}^n \left ( vCount_{p} \times \left ( \sum_{l=1}^m \text{dPieces}_{p,l} + \begin{cases} -1, & \text{if } \text{dWaste}_{p} \text{ = 0} \\ 0, & \text{otherwise} \end{cases} \right ) \right ) \tag{1} \\ \\ &\text{Subject to} \\ & \quad \text{dDemand}_{l} \quad &= &\quad \sum_{p=1}^n vCount_{p} \times \text{dPieces}_{p,l} & \quad \forall \ l \in L \tag{2} \\ & \quad vCount_{p} \quad &\le &\quad vUsePattern_{p} \times \text{dAvailable} & \quad \forall \ p \in P \tag{3} \\ \\ &\text{Variables} \\ & \quad vCount_{p} &= &\quad \text{Number of times pattern used} & \quad \forall \ p \in P \tag{4} \\ & \quad vUsePattern_{p} &= &\quad \begin{cases} 1, &\text{if pattern \(p\) is used} \\ 0, &\text{otherwise} \tag{5} \end{cases} \quad &\forall \ p \in P \\ \\ &\text{Data} \\ & \quad \text{dWeight}_{1, 2, \text{ or } 3} &= &\quad \text{Weight on objective function component} \tag{6} \\ & \quad \text{dPieces}_{p,l} &= &\quad \text{Number of pieces of each length in each pattern} & \quad \forall \ p \in P, \forall \ l \in L \tag{7} \\ & \quad \text{dDemand}_{l} &= &\quad \text{Number of each length required} & \quad \forall \ l \in L \tag{8} \\ & \quad \text{dAvailable} &= &\quad \text{Large constant, as availability unlimited} \tag{9} \\ \\ &\text{Sets} \\ & \quad L &\ &\quad \text{Length} \tag{10} \\ & \quad P &\ &\quad \text{Pattern} \tag{11} \\ \\ &\text{Dimensions} \\ & \quad m &\ &\quad \text{Number of Lengths} \tag{12} \\ & \quad n &\ &\quad \text{Number of Patterns} \tag{13} \\ \\ &\text{Bounds} \\ & \quad \text{Non-negative} &\ &\quad \tag{14} \\ \end{alignat*}

Implementation

Decide how many of each cutting pattern to use

The essence of this model is shown in Figure 4, which shows the first few cutting patterns. For example, Pattern 4800-1 cuts 2 x Piece A, with waste of 168 mm, and Pattern 4800-2 cuts one each of Piece A and Piece B, with waste of 284 mm.

We have two variables for each pattern:

A binary decision about whether to use the pattern.
If we use a pattern, then an integer count specifying how many of that pattern to use.

From this list we can calculate how many of each size piece to cut, and the total waste that results from using the selected cutting patterns. For example, if we make 20 copies of Pattern 4800-1 and 100 copies of Pattern 4800-4, then we will have 140 of Piece A, 100 of Piece D, and 100 of Piece G. The total waste from those stock items will be 20x168 + 100x44 = 7,760 mm, which equates to 7,760 / (120x4,800) = 1.35% of the stock length.

Solver model

Objective function

The Solver model is shown in Figure 5.

In the paper, the objective is to minimize total waste. To enable us to explore alternative solutions, we extend the paper's objective to minimize a weighted average of three terms:

Total length of waste, in metres. This is the objective specified in the paper.
Number of cutting patterns used. To help with reducing operational complexity, it might be useful to minimize the number of different patterns used.
Total number of cuts made. We assume that more cuts require more effort and/or time. Therefore, it may be useful to minimize the number of cuts.

Weights on the objective terms of 1.000, 0.100, and 0.010 respectively work well with the current data. We want to minimize each of the terms, so all three weights are positive. To replicate the model as specified in the paper, we can set the second and third weights to zero.

Variables

The model has two sets of variables:

vCount. The number of copies to make of each cutting pattern.
vUsePattern. Whether or not to use a cutting pattern.

Constraints

The constraints are:

fSupply = fDemand. Demand must be exactly met. This is quite an inflexible constraint, which the paper implies was not always being met prior to the case study.
vCount <= fUseUB. Supply of stock is assumed to be unlimited, so we multiply the vUse variable by a large number (9,999), leading to an upper bound on supply that is either zero or a large number.
vCount = integer. We make an integer number of cutting pattern copies.
vUsePattern = binary. We either use a cutting pattern or not.

Solution method

All the model's relationships are linear, so we can use the Simplex method for our Mixed Integer Linear Program (MILP).

This model is too large for Solver, so we need to use OpenSolver. The solution time is usually a few seconds, though it is possible to construct assumptions that take much longer to solve to optimality.

Analysis

Scenarios

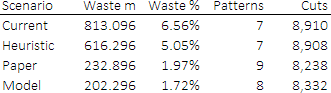
We've analyzed four scenarios. A summary of the scenario results is shown in Figure 6:

Current. The current cutting plan, as described in the paper, using a heuristic to decide how to cut the stock pieces. That is, cut only one size of pieces from each stock item. Since there are seven lengths needed, this plan requires seven patterns. The total off-cut length is 813.096 m, which equates to 6.56% waste.
Heuristic. The current plan can be improved by applying the same heuristic. That is, changing the plan for pieces E and G produces a significant reduction in waste.
Paper. The solution presented in the paper is a substantial improvement on the current scenario, with 1.97% waste.
Model. The result of our optimization model, which further reduces the waste to 1.72%.

Surprisingly, our model's solution is materially better than the solution from the paper's model. It is not clear why, as the paper's solution is feasible – but not optimal – in our implementation. We speculate that the procedure that the paper's authors used to generate the potential cutting patterns inadvertently excluded some patterns that our implementation included. The paper's lead author was contacted for comment, but no reply has been received.

Note that the total off-cut of 202.296 metres in our solution looks like a lot of waste – but it is only about 200 metres out of over 11 kilometres of total demand. Importantly, this is a 75% reduction in waste relative to the current practice. Given that the purpose of this case study is to reduce waste, this is an excellent outcome.

Exploring other solutions

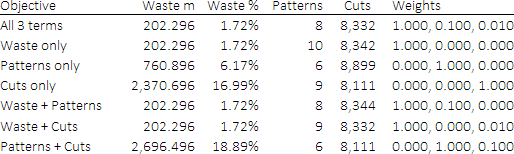
We extended the paper's formulation by including three objective function terms: the total length of waste, number of cutting patterns used, and total number of cuts made to produce all the pieces.

By changing the weights for the three terms, we can obtain a variety of different solutions – some of which are shown in Figure 7. Specifically, we looked at the following cases:

All 3 terms. This is the solution described above. The objective function has the largest weight on the waste, but also provides good – though not necessarily minimal – results for the other two terms.
Waste only. By putting zero weights on the number of patterns and number of cuts, we're telling the solver to ignore those terms. The waste is minimized, but the other terms have worse results.
Patterns only. It turns out that we can fulfil the customer's requirements for wood pieces by using only 6 patterns, rather than the 8 patterns we used in the "All 3 terms" case. However, this is achieved by significantly increasing the amount of waste (though still less than the waste in the current situation). The CBC solver had difficulty proving that 6 is the minimum number of patterns, so we used the commercial CPLEX solver instead.
Cuts only. We can also reduce the number of cuts required, but at the expense of a large increase in the amount of waste. This trade-off is unlikely to be acceptable.
Waste + Patterns. This solution is very similar to the "All 3 terms" case, though with slightly more cuts required.
Waste + Cuts. This solution is also very similar to the "All 3 terms" case.
Patterns + Cuts. By ignoring the amount of waste, we get minimal values for both the number of patterns and the number of cuts. However, the large amount of waste is unlikely to be acceptable. We again used CPLEX to solve this variant of the model.

These cases illustrate the impact of putting different weights, or emphasis, on each of the terms in the objective function. Given the purpose of minimizing waste, the first case – all three terms, with the highest weight on the length of waste – is considered to provide the best trade-off between the objectives.

The cases also show that some variations of a model are much more difficult to solve. For two of the cases we used the commercial CPLEX solver via the NEO online portal, as the free CBC solver had difficulty finding an optimal solution in a reasonable time. Being able to access other solvers via NEOS is very useful – a topic that we will explore further in a later article.

Conclusion

This article replicates, and improves, the results of a case study published in an academic paper.

Our analysis explores a range of model behavior by changing the weights on each term in the objective function. Different weights put emphasis on each term relative to the others, leading to different trade-offs.

More generally, the pattern selection formulation technique used in this model is applicable to a wide range of situations, including cutting, packing, scheduling, and location problems. We will use this type of technique again, in an upcoming example model blog article.

If you would like to know more about this model, or you want help with your own models, then please contact us.

References

This article is based on the paper:

Wattanasiriseth, P. & Krairit, A. (2019). "An application of cutting-stock problem in green manufacturing: A case study of wooden pallet industry", 2019 IOP Conference Series: Materials Science and Engineering, 530 012005.

Green manufacturing via cutting patterns